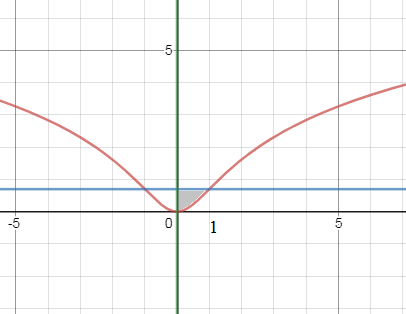
Задача 44937 Найти площадь фигуры ограниченной...
Условие
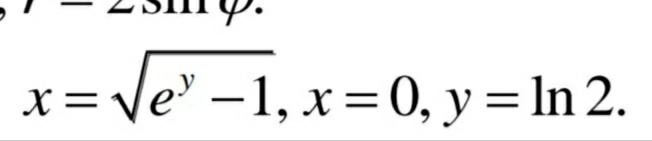
математика ВУЗ
786
Решение
★
sqrt(e^(y)-1)=t
e^(y)-1=t^2
e^(y)=t^2+1
y=ln(t^2+1)
dy=2tdt/(t^2+1)
y=ln2 ⇒ t=sqrt(e^(ln2)-1)=sqrt(2-1)=1
y=0 ⇒ t=sqrt(e^(0)-1)=sqrt(1-1)=0
S= ∫ ^(1)_(0)[b]([/b]t*(2tdt/(t^2+1))[b])[/b]=
=∫ ^(1)_(0)(2t^2+2-2)dt/(t^2+1)=
=∫ ^(1)_(0)2dt-2∫ ^(1)_(0)dt/(t^2+1)=
=(2t)|^(1)_(0)-(2arctgt)|^(1)_(0)=2*1-2arctg1=2-2*(π/4)=[b]2-(π/2)[/b]