Задача 44828 15-го декабря планируется взять кредит в...
Условие
— 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца с 1-го по 10-й долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца;
— к 15-му числу 11-го месяца кредит должен быть полностью погашен.
Какой долг будет 15-го числа 10-го месяца, если общая сумма выплат после полного погашения кредита составит 1231 тысячи рублей?
Решение
(1000 - X) тыс. руб. будет выплачено за 10 месяцев
Делим на 10:
[m]\frac{1000-X}{10}[/m] тыс руб - [b]ежемесячное [/b] погашение основного долга
таким образом с15–го числа каждого месяца с 1–го по 10–й долг будет на одну и ту же сумму меньше долга на 15–е число предыдущего месяца, а именно на [m]\frac{1000-X}{10} [/m]
И каждый месяц выплата процентов на остаток
За [i]первый[/i] месяц проценты составят:
0,03*1000 тыс руб=30 тыс руб.
За [i]второй [/i]месяц.
Сумма долга уменьшится на [m]\frac{1000-X}{10} [/m] и остаток долга составит:
(1000 - [m]\frac{1000-X}{10} [/m] =[m]\frac{9\cdot 1000+X}{10}[/m] тыс руб
Проценты на остаток:
0,03* [m]\frac{9\cdot 1000+X}{10}[/m] тыс руб
За [i] третий[/i] месяц
Сумма долга опять уменьшится на [m]\frac{1000-X}{10} [/m] и остаток долга составит:
1000 - [m]\frac{1000-X}{10} [/m]- [m]\frac{1000-X}{10} [/m]=[m]\frac{8\cdot 1000+X}{10}[/m] тыс руб
Проценты на остаток:
0,03* [m]\frac{9\cdot 1000+X}{10}[/m]
и так далее
За 10-й месяц долг:
[m]\frac{1000+X}{10}[/m] тыс руб
Проценты на остаток:
0,03* [m]\frac{1000+X}{10}[/m] тыс руб
За 11-й месяц остаток Х
Проценты на этот остаток: 0,03*X тыс руб
Сумма выплат 1231 состоит из взятого кредита 1000 ( деленного на равные части 10 месяцев и Х) и начисленных процентов.
Выплата процентов составит:
1231-1000=[b]231[/b] тыс руб.
Составляем уравнение:
30+ 0,03* [m]\frac{9\cdot 1000+X}{10}[/m]+0,03*[m]\frac{8\cdot 1000+X}{10}[/m] + ... +0,03* [m]\frac{1000+X}{10}[/m] + 0,03X=[b]231[/b]
0,03* ( [m]\frac{9\cdot 1000+X}{10}+\frac{8\cdot 1000+X}{10} + ... +\frac{1000+X}{10}[/m] ) + 0,03X=[b]201[/b]
Применяем формулу суммы n членов арифметической прогрессии:
(X/10)+(2Х/10)+... +(9Х/10)=(1/10)*(Х+9Х)*9/2)=4,5Х
(9*1000/10 + 8*1000/10 + ... + 1000/10)=(1/10)*(1000+9000)*9/2=45
0,03*(4500+4,5Х)+0,03Х=201
0,165*Х=66
X=400
О т в е т. 400 тыс руб.
[b]Второй способ.[/b]
Кредит на [b]11 месяцев.[/b]
1)[i] условие [/i]
–1–го числа каждого месяца долг увеличивается на 3% по сравнению с концом предыдущего месяца
См первый столбик ( начисление процентов на долг)
2) [i]условие [/i]
– со 2го по 14–е число каждого месяца необходимо [b]выплатить одним платежом часть долга;[/b]
[red]и так, чтобы
выполнялось условие [/red]
3)[i] условие [/i]
15–го числа каждого месяца с 1–го по 10–й долг должен быть [b]на одну и ту же сумму меньше долга [/b]на 15–е число [b]предыдущего месяца;[/b]
Это показано в правом столбце таблицы
4) долг в конце 10-го месяца [b]неизвестен.[/b]
Обозначим его [b]А[/b] тыс руб.
Решаем задачу, так называемым [i]"методом решения задачи с конца" [/i]
Пусть долг ежемесячно уменьшается на одну и ту же величину[b] х [/b] тыс руб
Тогда в конце 10-го месяца он составит [b](A+х) [/b] тыс руб
В конце 9-го месяца долг составит[b] (A+2х) [/b]тыс. руб
.....
В конце первого месяца от будет [b](A+9x)[/b] тыс руб
И поскольку согласно условия 3) долг и за 1-ый месяц уменьшился на х тыс. руб, то значит
[/b] сумма кредита составляет [b](A+10х)[/b] тыс руб
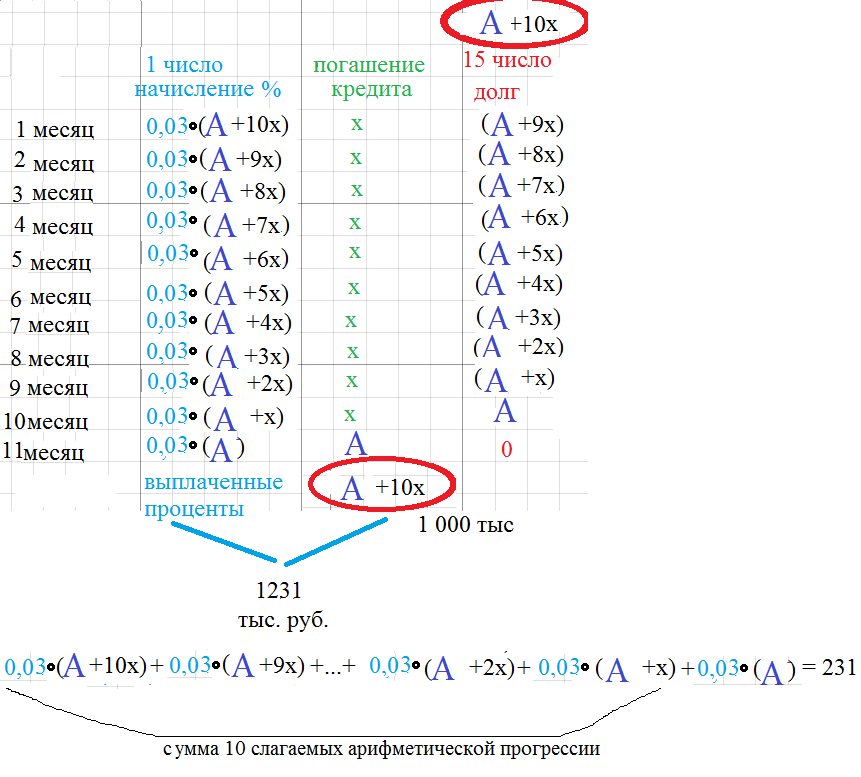
В первом столбце показано как начисляют проценты.
[i]Проценты[/i] начисляют [/b] на остаток долга[/b]
Поэтому за [b] 1-ый месяц проценты[/b] начислены на весь кредит.
[green]3%=0,03[/green]
[green]0,03[/green]*([b]A+10x[/b]) тыс руб - проценты, начисленные за [i]первый[/i] месяц
[b]Клиент выплачивает[/b] со 2-го по 14-е число первого месяца :
([green]0,03[/green]*([b]A+10x[/b])+ [b]x [/b] )тыс. руб
[i]При таких выплатах[/i] остаток долга уменьшится на х тыс. руб.
[b]Цикл повторяется 10раз[/b]
Уравнение:
[green]0,03[/green]*(А+10x)+[b]x[/b]+ [green]0,01[/green]*(А+9x)+x+[green]0,03[/green]*(А+8x)+[b]x[/b]+...+[green]0,03[/green]*(А) +[b]А[/b]=1231
[green]0,03[/green]*(11А+10x+9x+...+x)+[b]10*x[/b]+А=1231
10x+A=1000 (это cумма кредита) ⇒ 10*x=1000-A
[green]0,03[/green]*(11A)+[green]0,03[/green]*(10x+9x+...+x)=231
в скобках сумма 10-ти членов арифметической прогрессии
[green]0,03[/green]* (11A)+[green]0,03[/green](10х+х)*10/2=231
0,33A+0,03*11*[b]10*x[/b]/2=231
Но 10*х=1000-A
0,33А+0,165*(1000-А)=231
0,165*А=231-165
0,165*А=66
A=400 тыс руб.
О т в е т. 400 тыс руб.