Задача 44523 15 декабря планируется взят кредит в...
Условие
— 1-го числа каждого месяца долг возрастает на 4% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца с 1 -го по n-й долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца;
— 15-го числа n-го месяца долг составит 400 тысяч рублей;
— к 15-му числу (n+1)-го месяца кредит должен быть полностью погашен.
Найдите га, если известно, что общая сумма выплат после полного погашения кредита составит 3248 тысяч рублей.
Все решения
1)[i] условие [/i]
–1–го числа каждого месяца долг увеличивается на 4% по сравнению с концом предыдущего месяца
[blue]4%=0,04[/blue]
См первый столбик ([i]ежемесячное[/i] начисление процентов [b]на остаток долга[/b])
2) [i]условие [/i]
– со 2го по 14–е число каждого месяца необходимо [b]выплатить одним платежом часть долга;[/b]
[red]и так, чтобы
выполнялось условие [/red]
3)[i] условие [/i]
15–го числа каждого месяца с [red]1[/red]–го по [red]n[/red]–й месяц долг должен быть [b]на одну и ту же сумму меньше долга [/b]на 15–е число [b]предыдущего месяца;[/b]
Это показано в правом столбце таблицы
4)[i] условие [/i]
15–го числа [red]n [/red]–го месяца долг составит [blue]400[/blue] тысяч рублей
С него и начинаем решать задачу, так называемым [i]"методом решения задачи с конца" [/i]
Пусть долг ежемесячно уменьшается на одну и ту же величину[b] х[/b] тыс руб
Тогда в конце [red](n-1)[/red]-го месяца он составит ([blue]400[/blue]+[red]1[/red]*[b]х[/b]) тыс руб.
В конце [red](n-2)[/red]-го месяца долг составит ([blue]400[/blue]+[red]2[/red]*[b]х[/b]) тыс руб.
.....
В конце первого месяца от будет ([blue]400[/blue]+[red](n-1)[/red]*[b]х[/b]) тыс руб.
И поскольку согласно условия 3) долг и за 1-ый месяц уменьшился на х тыс. руб, то значит
сумма кредита составляет ([blue]400[/blue]+[red]n[/red]*[b]х[/b]) тыс руб.
В первом столбце- начисление процентов.
[b]Проценты начисляют на остаток долга[/b]
Поэтому за [b] 1-ый месяц проценты[/b] начислены на весь кредит.
4%=[green]0,04[/green]
[green]0,04[/green]* ([blue]400[/blue]+[red]n[/red]*[b]х[/b]) тыс руб - проценты , начисленные
в [i]первый[/i] месяц
[b]Клиент выплачивает[/b] со второго по 14 число[i] первого[/i] месяца :
эти проценты и часть кредита x тыс руб
[green]0,04[/green]* ([blue]400[/blue]+[red]n[/red]*[b]х[/b]) + [b]х[/b]
[i]При таких условиях выплаты[/i] остаток долга уменьшится на х тыс. руб.
и станет равным ([blue]400[/blue]+[red](n-1)[/red]*[b]х[/b]) тыс руб.
Первого числа [i]второго месяца [/i] начисляют проценты на этот остаток:
[green]0,04[/green]* ([blue]400[/blue]+[red](n-1)[/red]*[b]х[/b]) тыс руб. - проценты , начисленные во [i]второй [/i]месяц
[b]Клиент выплачивает[/b] со второго по 14 число [i]второго[/i] месяца :
эти проценты и часть кредита [b]x[/b] тыс руб
[green]0,04[/green]* ([blue]400[/blue]+[red](n-1)[/red]*[b]х[/b] + [b]х[/b]
и остаток долга снова уменьшится на [b]х[/b] тыс. руб. и станет равным
([blue]400[/blue]+[red](n-2)[/red]*[b]х[/b])
[b]Цикл повторяется n раз[/b]
По условию задачи общая сумма выплат 3248 руб. Из них 2000 взятый кредит, значит по процентам выплачено 1248 тыс руб .
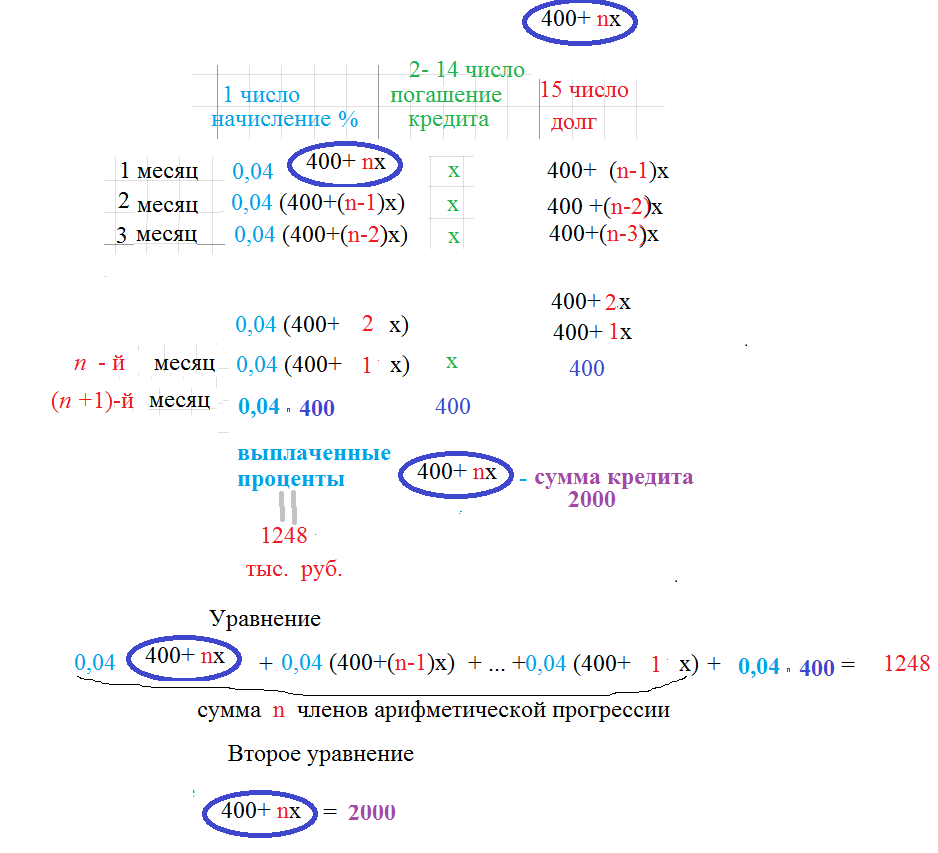
Складываем слагаемые первого столбца и получаем уравнение:
[green]0,04[/green]* ([blue]400[/blue]+[red]n[/red]*[b]х[/b]) +
+[green]0,04[/green]* ([blue]400[/blue]+[red](n-1)[/red]*[b]х[/b])+
...
+[green]0,04[/green]* ([blue]400[/blue]+[red]2[/red]*[b]х[/b]) +
+[green]0,04[/green]* ([blue]400[/blue]+[red]1[/red]*[b]х[/b])+
+[green]0,04[/green]*[blue]400[/blue]= [b]1248[/b]
Слева (n+ 1) -слагаемое, выплата процентов проводилась в течении всего срока кредита, в течении
(n+1) месяца
[green]0,04[/green]*([blue]400[/blue]*[red]n [/red]+([red]n-1[/red])+...+2+1)+[green]0,04[/green]*[blue]400[/blue]=1248
В скобках [b]сумма n- членов арифметической прогрессии[/b]
[green]0,04[/green]*[blue]400[/blue]*[red]n [/red]+ [green]0,04[/green]x*[m]\frac{1+n}{2}\cdot n[/m] +16=1248
0,04*[blue]400[/blue]*n+0,02*[red]n[/red]*([red]n+1[/red])[b]x[/b]=1232
Так как сумма кредита известна , то составим второе уравнение:
[blue]400[/blue]+[red]n[/red]*[b]х[/b]=2000 ⇒ из которого [red]n[/red]*[b]х[/b]=1600
подставим в первое вместо nx
0,04*400*[red]n[/red]+0,02*[b]n[/b]*([red]n+1[/red])[b]x[/b]=1232
16n+0,02*1600*(n+1)=1232
16n+32(n+1)=1232
48n=1200
n=25
О т в е т. 25 месяцев