Задача 43437 Вычислить пределы функций, не...
Условие
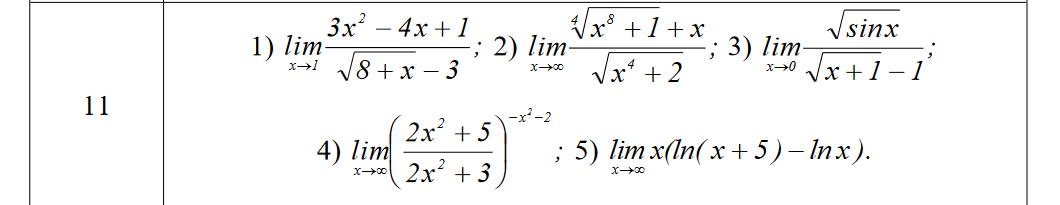
Решение
Неопределенность 0/0
Числитель раскладываем на множители:
3x^2-4x+1=(3x-1)(x-1)
Умножаем и числитель и знаменатель на выражение
sqrt(8+x)+3
Получаем:
[m]=\lim_{x \to 1}\frac{(3x-1)(x-1)(\sqrt{8+x}+3)}{(\sqrt{8+x}-3)(\sqrt{8+x}+3)}=[/m]
Применяем формулу разности квадратов a^2-b^2=(a-b)*(a+b)
[m]\lim_{x \to 1}\frac{(3x-1)(x-1)(\sqrt{8+x}+3)}{(\sqrt{8+x})^2-3^2}=\lim_{x \to 1}\frac {(3x-1)(x-1)(\sqrt{8+x}+3)}{8+x-9}=[/m]
[m]=\lim_{x \to 1}\frac {(3x-1)(x-1)(\sqrt{8+x}+3)}{x-1}=[/m]
Сокращаем (на x-1)
[m]=\lim_{x \to 1}(3x-1)(\sqrt{8+x}+3)=(3\cdot 1 -1)(\sqrt{8+1}+3)=[/m]
[m]=2\cdot 6=12[/m]
2) Неопределенность ( ∞ / ∞ )
Делим и числитель и знаменатель на x^2
[m]=\lim_{ \to \infty }\frac{\frac{\sqrt[4]{x^8+1}+x}{x^2}}{\frac{\sqrt{x^4+2}}{x^2}}=[/m]
Делим почленно, те каждое слагаемое числителя делим на x^2 и
каждое слагаемое знаменателя делим на x^2:
[m]\lim_{ \to \infty }\frac{\frac{\sqrt[4]{x^8+1}}{x^2}+\frac{x}{x^2}}{\frac{\sqrt{x^4+2}}{x^2}}[/m]
Применяем свойства корня:
[m]\lim_{\to \infty }\frac{\sqrt[4]{\frac{x^8+1}{x^8}}+\frac{x}{x^2}}{\sqrt{\frac{x^4+2}{x^4}}}=[/m]
[m]\lim_{\to \infty }\frac{\sqrt[4]{1+\frac{1}{x^8}}+\frac{1}{x}}{\sqrt{1+\frac{2}{x^4}}}=\frac{\sqrt[4]{1+0}+0}{\sqrt{1+0}}=1[/m]
3) Неопределенность (0/0)
Умножаем и числитель и знаменатель на
sqrt(x+1)+1
[m]\lim_{x\to 0 }\frac{\sqrt{sinx}\cdot(\sqrt{x+1}+1)}{(\sqrt{x+1}-1)(\sqrt{x+1}+1)}=[/m]
Применяем формулу разности квадратов и получаем:
[m]\lim_{x\to 0 }\frac{\sqrt{sinx}\cdot(\sqrt{x+1}+1)}{x}=\lim_{x\to 0 }\frac{\sqrt{sinx}}{\sqrt{x}}\cdot \frac{\sqrt{x+1}+1}{\sqrt{x}}=1\cdot\frac{\sqrt{0+1}+1}{0}=\infty[/m]