Задача 43207 1.Найти площадь фигуры, ограниченной...

vk163865655

2019-12-29 21:07:58

1.Найти площадь фигуры, ограниченной линиями
Желательно с подробным объяснением

sova

2019-12-29 21:45:41

★

1)
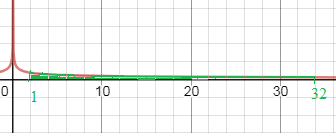
S= ∫ ^(32)_(1)x^(-0,4)dx=[m]\frac{x^{-0,4+1}}{-0,4+1}[/m]|^(32)_(1)=

=[m]\frac{x^{0,6}}{0,6}[/m]|^(32)_(1)=[m]\frac{32^{0,6}}{0,6}-\frac{1^{0,6}}{0,6}[/m]=[m]\frac{2^{5\cdot 0,6}}{0,6}-\frac{1^{0,6}}{0,6}=[/m]

=[m]\frac{2^{3}}{0,6}-\frac{1^{0,6}}{0,6}=\frac{8-1}{0,6}=\frac{35}{3}[/m]

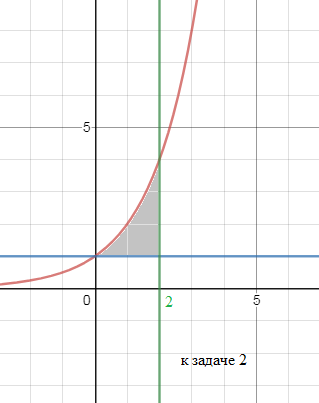
2)
S= ∫ ^(2)_(0)(2^(x)-1)dx=[m]\frac{2^{x}}{ln2}-x[/m]|^(2)_(0)=

=[m]\frac{2^{2}}{ln2}-\frac{2^{0}}{ln2}-(2-0)=]\frac{4-1}{ln2}-2=\frac{3}{ln2}-2[/m]

3)
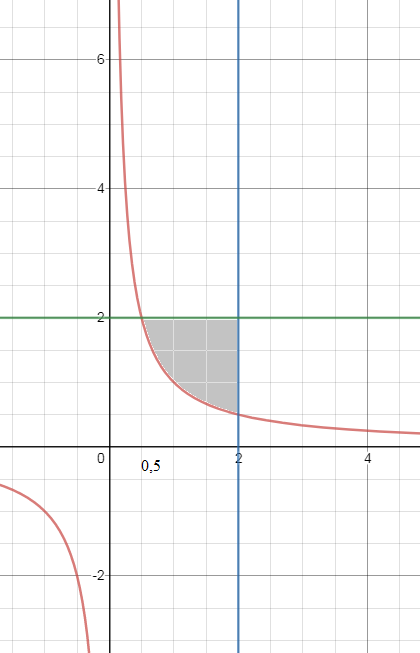
S= ∫ ^(2)_(0,5) (2-[m]\frac{1}{x}[/m])dx=

=(2x-ln|x|)|^(2)_(0,5)= 2*2-ln2-(2*0,5-ln0,5)=3-ln2+ln0,5=3-ln2+ln2^(-1)=

=3-ln2-ln2=3-2ln2

4)

S= ∫ ^(0)_(-1)(1+e^(x))dx=(x+e^(x))|^(0)_(-1)=0+e^(0)- (-1+e^(-1))=

=0+1+1-(1/e)=[b]2-(1/e)[/b]