Задача 43161 составить параметрические уравнения...

lage90

2019-12-27 02:07:00

составить параметрические уравнения прямой, проходящей через точку М1(1,0,-3) параллельно прямой (х-1)/2= (y+1)/-3=(z-7)/3

sova

2019-12-27 15:03:26

Дано каноническое уравнение прямой

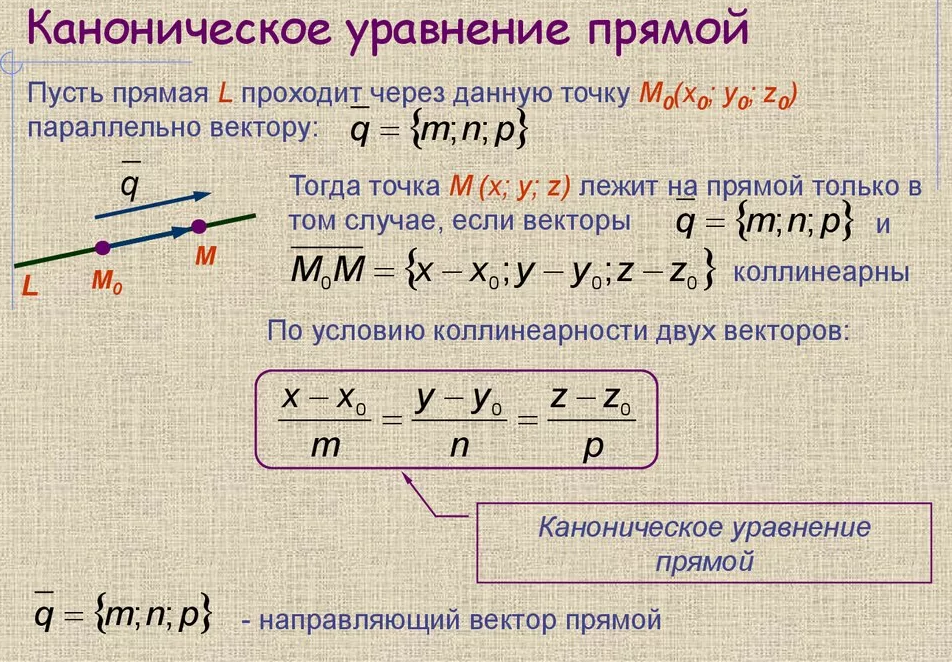
[m]\frac{x–1}{2}=\frac{y+1}{-3}=\frac{z-7}{3}[/m]
это уравнение прямой, проходящей через точку
Mo(1;-1;7)
с направляющим вектором vector{q}=(2;-3;3)

Параллельные прямые имеют коллинеарные направляющие векторы (можно считать, что направляющие векторы одинаковые )

Уравнение искомой прямой, как прямой, проходящей через точку

M_(1)(1;0;-3) с направляющим вектором vector{q}=(2;-3;3)

имеет тот же вид:

[m]\frac{x–1}{2}=\frac{y-0}{-3}=\frac{z-(-3)}{3}[/m]

О т в е т. [m]\frac{x–1}{2}=\frac{y}{-3}=\frac{z+3}{3}[/m]