Задача 42909 10. Найти экстремумы функции...

annarudnik

2019-12-19 22:55:31

10. Найти экстремумы функции y=(x+2)^2(x-1) точки перегиба, ее график и построить эскиз графика.

11. Провести полное исследование функции y = (x-1)^2/(x^2+1) и построить ее график

sova

2019-12-20 00:07:20

★

1.D(y)=(–∞;+ ∞)
Вертикальных асимптот нет

Функция не является ни четной, ни нечетной
lim_(x→ +∞)f(x)=+∞

lim_(x→–∞)f(x)= -∞

горизонтальной асимптоты нет


y`=((x+2)^2)`*(x-1)+(x+2)^2*(x-1)`
y`=2(x+2)*(x-1)+(x+2)^2*1
y`=(x+2)*(2x-2+x+2)
y`=3x(x+2)

y`=0

x=0; x=-2

_+__ (-2) __-_ (0) _+__

y`< 0 при x∈ (–2;0)
Функция [i]убывает[/i] при x∈ (–2;0)

y`>0 при x∈(-∞;-2) и при х∈ (0;+∞)
Функция [i]возрастает[/i] при x∈(-∞;-2) и при х∈ (0;+∞)

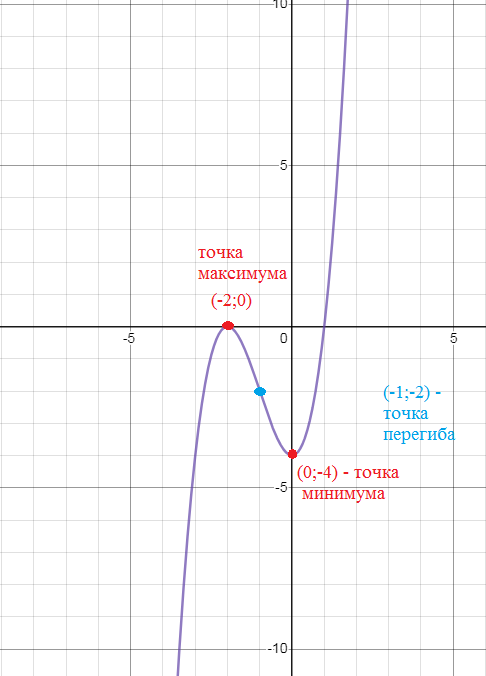
x=0– точка минимума, производная меняет знак с – на +
у(0)=-4 - [i]наименьшее[/i] значение функции

x=-2 - точка максимума
y(-2)=0 -[i] наибольшее[/i] значение функции

y``=(3x^2+6x)`=6x+6
y``=0
x=-1- точка перегиба

y`` <0 на ( - ∞ ;-1) ⇒
Функция выпукла вверх на ( - ∞ ;-1)

y`` > 0 на
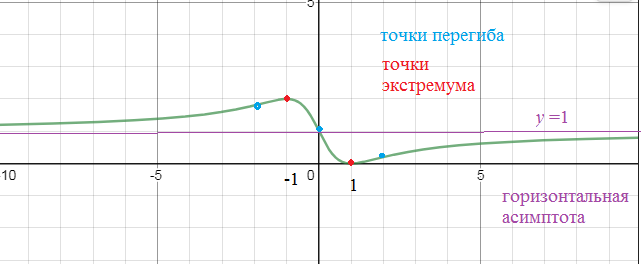
Функция выпукла вниз на (-1;+ ∞)
2.
1) D(y)=(–∞;+ ∞)
Вертикальных асимптот нет

2) Функция не является ни четной, ни нечетной
у(–х)=(–х-1)^2/((–x)^2+1)=(х+1)^2/(x^2+1)
y(–x) ≠ y(x)
y(–x) ≠- y(x)
3)lim_(x→ +∞)f(x)=lim_(x→ +∞)(х-1)^2/(x^2+1)=1

lim_(x→–∞)f(x)=lim_(x→ -∞)(х-1)^2/(x^2+1)=1

y=1 -[i] горизонтальная асимптота[/i]

Наклонной асимптоты нет, так как
k=limx→∞(f(x))/x=0

4) Точки пересечения с осями координат
С осью ОХ
f(x)=0
(x-1)^2/(x^2+1)=0
(x-1)^2=0
x-1=0
x=1

(1;0)-точка пересечения с осью Ох.

C осью Оу
х=0 ⇒ у=(-1)^2/1=1

(0;1)-точка пересечения с осью Оу.

5)
y`=((x-1)^2)`*(x^2+1)-(x^2+1)`*(x-1)^2)/(x^2+1)^2;
y`=(2(x-1)*(x^2+1)-2х*(x-1)^2)/(x^2+1)^2;

y`=2(х-1)(х+1)/(x^2+1)
y`=0
x-1=0 или x+1=0
x=1 или x=-1

Знак производной

__ + __ (-1) _–_ (1) ___+__

y`< 0 при x∈ (–1;1)
Функция [i]убывает[/i] при x∈ (–1;1)

y`>0 при x∈(-∞;-1) и при х∈ (1;+∞)
Функция [i]возрастает[/i] при x∈(-∞;-1) и при х∈ (1;+∞)


x=1– точка минимума, производная меняет знак с – на +
у(1)=0 - [i]наименьшее[/i] значение функции

x=-1 - точка максимума
y(-1)=2 -[i] наибольшее[/i] значение функции


6)y``=(2(x^2-1)`*(x^2+1)-2(x^2-1)(x^2+1)`)/(x^2+1)^2


y``=(2x*(-x^2+3)/(x^2+1)^2
y``=0

x=0; x=± √3 –точки перегиба,

вторая производная при переходе через точки меняет знак .

Функция выпукла вниз на (– ∞ ; - √3 ) и на (0;√3)

выпукла вверх на ( - √3;0 ) и на (√3 ;+ ∞ )