Задача 42899 Найти радиус сходимости...
Условие
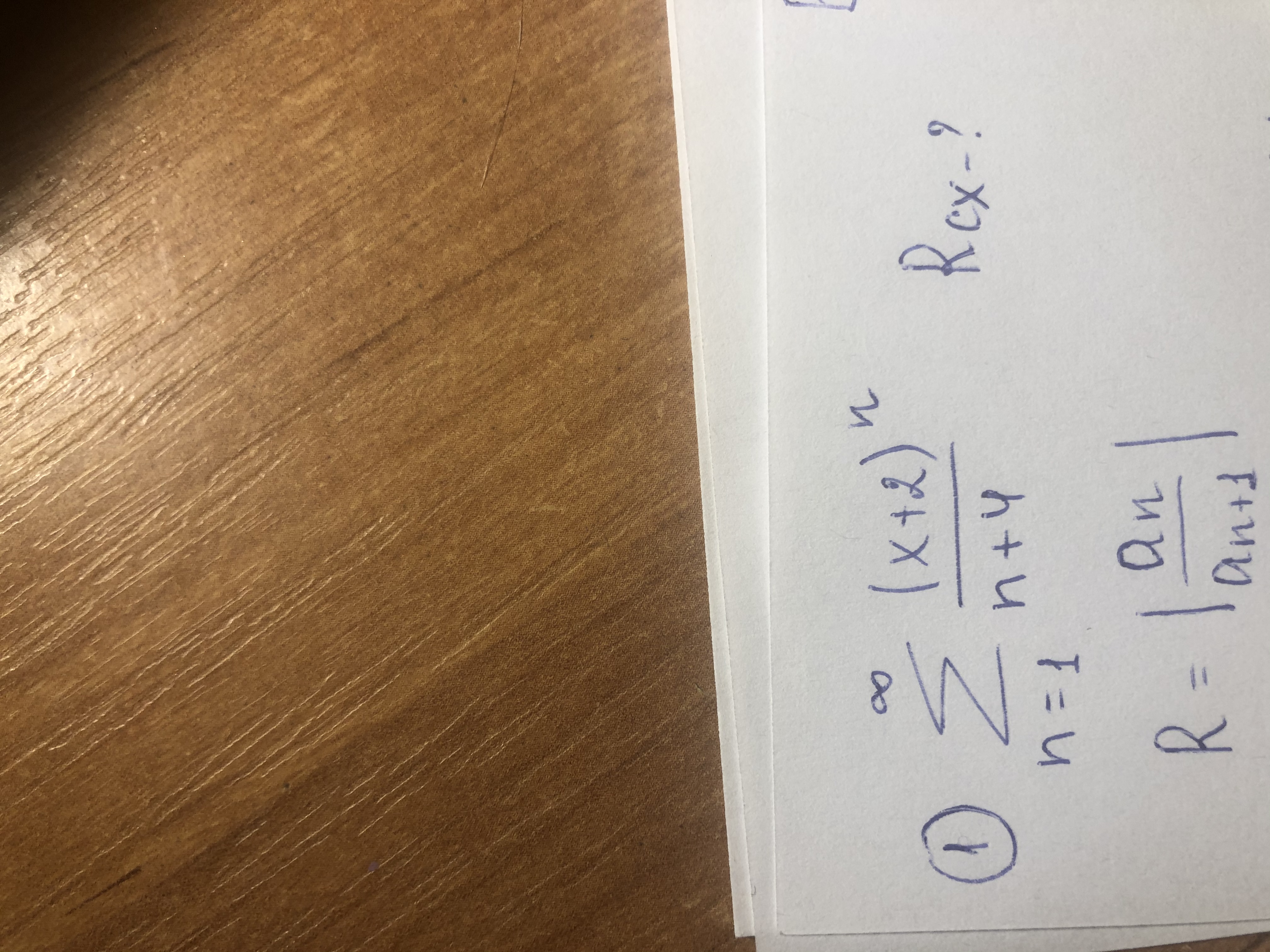
математика ВУЗ
889
Решение
★
∑ a_(n)*(x+2)^n,
где
a_(n)=1/(n+4)
тогда
a_(n+1)=1/((n+1)4)=1/(n+5)
R=lim_(n → ∞ )((a_(n)/a_(n+1))|=lim_(n → ∞ )(n+5)/(n+4)=1
Из неравенства
|x+2| < 1 получаем
-1 < x+2 < 1
-3 < x < -1
(-3; -1) - интервал сходимости ряда
Чтобы найти область сходимости, нужно проверить как будет вести себя ряд на концах этого интервала
При x=-3
∑ (-1)^n/(n+4) - знакочередующийся[i] числовой[/i] ряд, который сходится по признаку Лейбница
При x=-1
∑ 1/(n+4) - знакоположительный[i] числовой[/i] ряд, который
расходится как гармонический.
Поэтому
[-3;1) - область сходимости ряда