Задача 42366 Исследовать на непрерывность, выяснить...
Условие
графически следующие функции: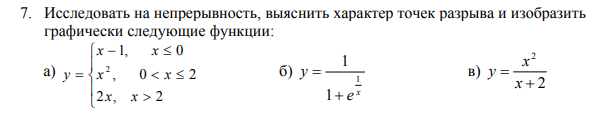 
Решение
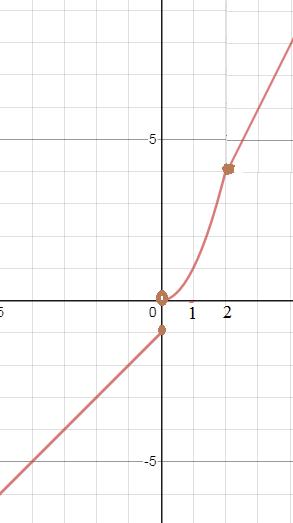
На (– ∞ ;0) функция непрерывна, так как y=x–1 непрерывна на (– ∞ ;+ ∞ )
На (0;2) функция непрерывна, так как y=x2 непрерывна на (– ∞ ;+ ∞ )
На (2;+ ∞ ) функция непрерывна, так как y=2x непрерывна на (– ∞ ;+ ∞ )
Значит, надо выяснить непрерывность функции в точке х=0 и х=2
Находим предел слева:
limx → –0f(x)=limx → –0(x–1)=–1
Находим предел справа:
limx → +0f(x)=limx → +0x2=0
предел слева ≠ пределу справа
Функция имеет скачок (конечный) в точке x=0
х=0 – точка разрыва первого рода
Находим предел слева:
limx →2 –0f(x)=limx → 2–0x2=4
Находим предел справа:
limx →2 +0f(x)=limx → 2+02x=4
х=2 – точка непрерывности
предел слева = пределу справа и равен значению функции в точке 2
f(2)=22=2
7б)
x ≠ 0
1+e1/x >0, так как et > 0 при любом t
Функция y=1/x непрерывна на (– ∞ ;0)U(0;+ ∞ )
Функция y=f(x) непрерывна на (– ∞ ;0)U(0;+ ∞ ) как композиция непрерывных функций.
Исследуем точку х=0
Находим предел слева:
limx → –0f(x)=1/1=1, так как
1/x → – ∞ при х → –0 ( слева от нуля, см график гиперболы y=1/x)
e1/x → 0 при x → –0, так как e– ∞ → 0
Находим предел справа:
limx →+0f(x)=0, так как
1/x → + ∞ при х → –0 ( слева от нуля, см график гиперболы y=1/x)
e1/x → 0 при x → –0, так как e– ∞ → 0
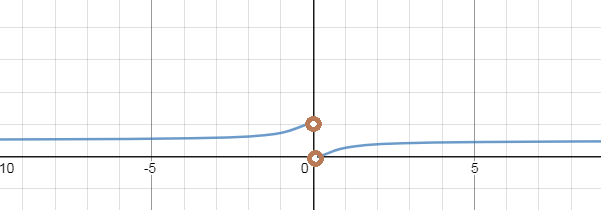
предел слева ≠ пределу справа
Функция имеет скачок (конечный) в точке
Значит х=0 – точка разрыва первого рода
7в)
x ≠ –2
При x ≠ –2 данная функция непрерывна как частное непрерывных функций.
Исследуем на непрерывность точку х=–2
Находим предел слева:
limx →–2–0f(x)=(–2–0)2/(–2–0+2)=– ∞ , так как
положительное число в числителе делится на очень маленькое в знаменателе.
Получим очень большое отрицательное (– ∞ )
Находим предел справа:
limx →2+0f(x)=(–2+0)2/(–2+0+2)=+ ∞
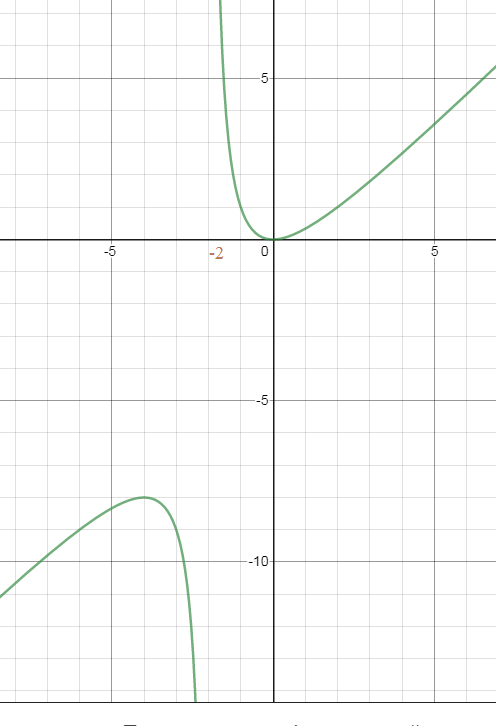
Функция имеет бесконечный предел в точке ( хотя бы один или слева или справа, а здесь вообще оба)
Значит х=–2 – точка разрыва второго рода
