Задача 41797 Помогите решить А и Б!!! Срочно надо ...

vk267309506

2019-11-21 21:22:07

Помогите решить А и Б!!!
Срочно надо

sova

2019-11-21 21:40:49

a)

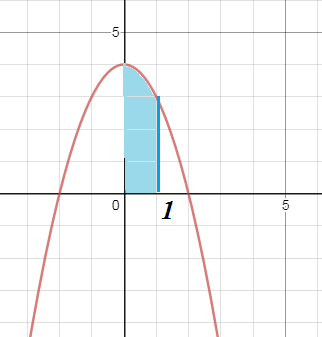
∫ ^(1)_(0)(4-x^2)dx=(4x-(x^3/3))|^(1)_(0)=4-(1/3)=11/3

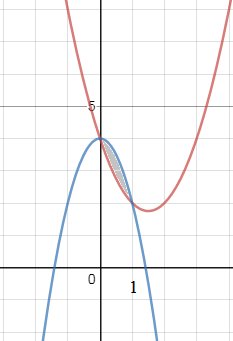
б)
Находим абсциссы точек пересечения кривых:

x^2-3x+4=4-2x^2

3x^2-3x=0

3x*(x-1)=0

Применяем формулу

[r]S= ∫ ^(b)_(a) (f(x)-g(x))dx[/r]

f(x)=4-2x^2
g(x)=x^2-3x+4


a=0;b=1


S= ∫ ^(1)_(0)((4-2x^2)-(x^2-3x+4))dx= ∫ ^(1)_(0)(3x-3x^2)dx=

=((3x^2/2)-3x)|^1_(0)=(3/2)-1=1/2=0,5