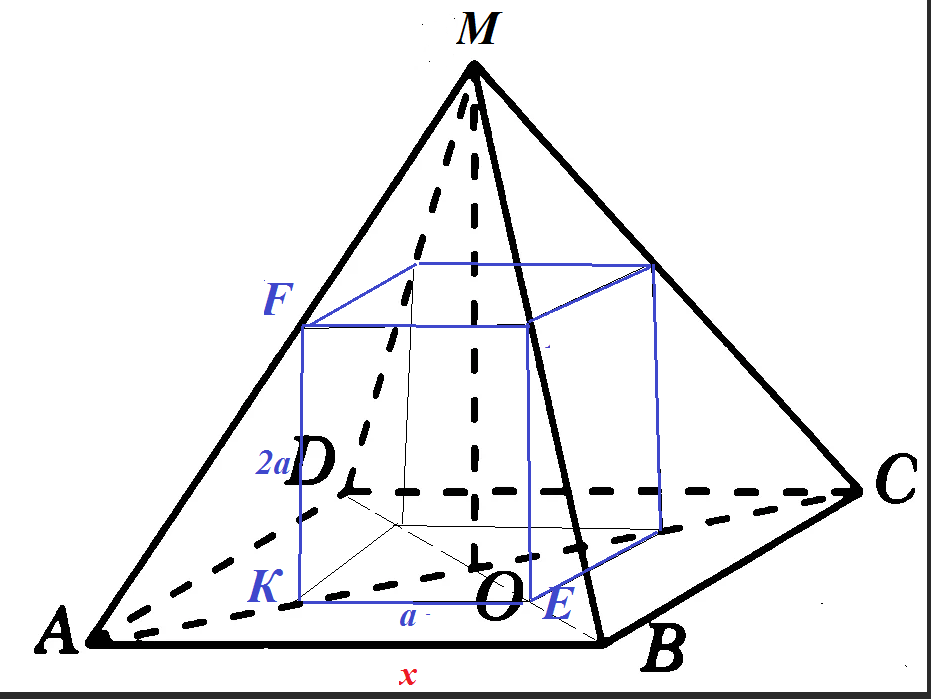
Задача 41758 Правильная четырехугольная призма и...

vk139625213

2019-11-20 21:51:32

Правильная четырехугольная призма и правильная четырехугольная пирамида расположены так, что одно из оснований призмы лежит в основании пирамиды, а вершины другого основания лежат на боковых ребрах пирамиды. Какой наименьший объем может иметь пирамида, если сторона основания призмы равна а, а боковое ребро равно 2а?

sova

2019-11-20 23:03:00

Пусть сторона основания пирамиды равна x


OK=asqrt(2)/2
OA=xsqrt(2)/2

AK=AO-KO=(x-a)sqrt(2)/2
KF:MO= AK:AO=(x-a)/x

KF=2a

MO=(2ax)/(x-a)

МО=Н

V_(пирамиды)=(1/3)*S_(осн)*Н=(1/3)*x^2*(2ax)/(x-a)

V_(пирамиды)=V(x)

V(x)=(2ax^3)/(3*(x-a)) - функция, зависящая от переменной х

Исследуем с применением производной:

V`(x)=(6ax^2*3*(x-a)-2ax^3*3)/(9(x-a)^2)

V`(x)=(12ax^3-18a^2x^2)/(9(x-a)^2)

V`(x)=0

12ax^3-18a^2x^2=0

12x-18a=0

x=3a/2


Это точка минимума, так как производная меняет знак с - на +

V(3a/2)=(2a/3)*(3a/2)^3/((3a/2)-a)=18a^3/4=[b]4,5a^3[/b]