Задача 41338 ...

sonya1666

2019-11-08 12:33:14

a) Решите уравнение [m]\cos x = \sqrt{\frac{1+\sin x}{2}}[/m].

б) Найдите его корни, принадлежащие отрезку [m]\left[3π; \frac{9π}{2}\right][/m].

sova

2019-11-08 13:11:05

По определению арифметического квадратного корня
значение корня есть число (выражение [i]неотрицательное[/i]), поэтому
cosx ≥ 0 ⇒ x в первой или четвертой четвертях

Возводим уравнение в квадрат:
cos^2x=(1+sinx)/2
2cos^2x=1+sinx

Так как
cos^2x=1-sin^2x

то уравнение примет вид:

2*(1-sin^2x)=1-sinx

Переносим правую часть влево и разложим на множители:

2*(1-sinx)*(1+sinx)-(1-sinx)=0


(1-sinx)*(2+2sinx-1)=0

(1-sinx)*(1+2sinx)=0
sinx=1 или 2sinx=- 1 ⇒ sinx=-1/2

[blue]x=(π/2)+2πn, n ∈ Z [/blue] или [blue]x=(-1)^(k+1)*(π/6)+πk, k ∈ Z[/blue]

Так как x в первой или четвертой четвертях, то
решение уравнения можно записать в виде:

[blue]x=(π/2)+2πn, n ∈ Z [/blue] или [blue]x=-(π/6)+2πk, k ∈ Z[/blue]

При n=2 получаем
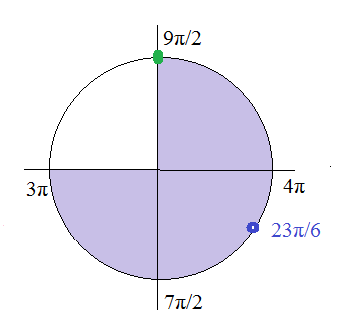
x=(π/2)+4π=9π/2 ∈ [3π; 9π/2]

При k=2 получаем
x=(-π/6)+4π=23π/6 ∈ [3π; 9π/2]

Указанному отрезку принадлежат корни : 23π/6; 9π/2
см. рис.