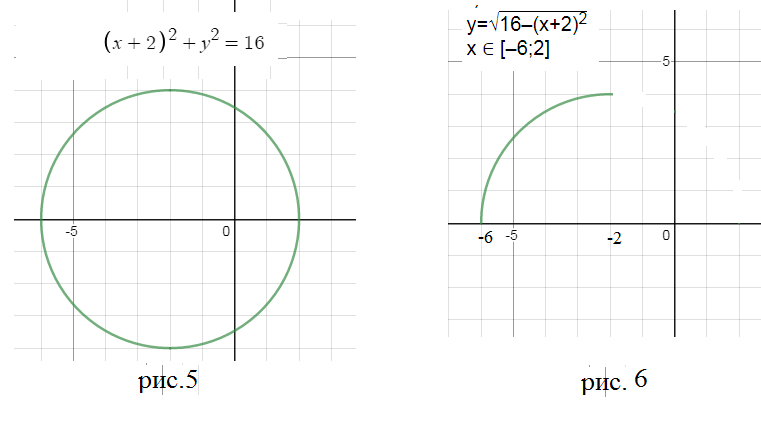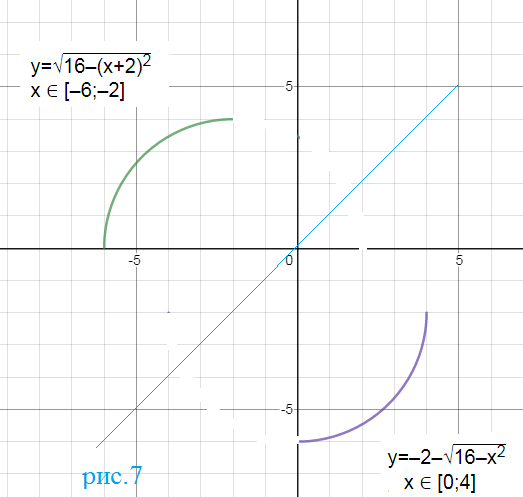Задача 40961 Постройте график функции y=f(x), найдите...
Условие

Решение
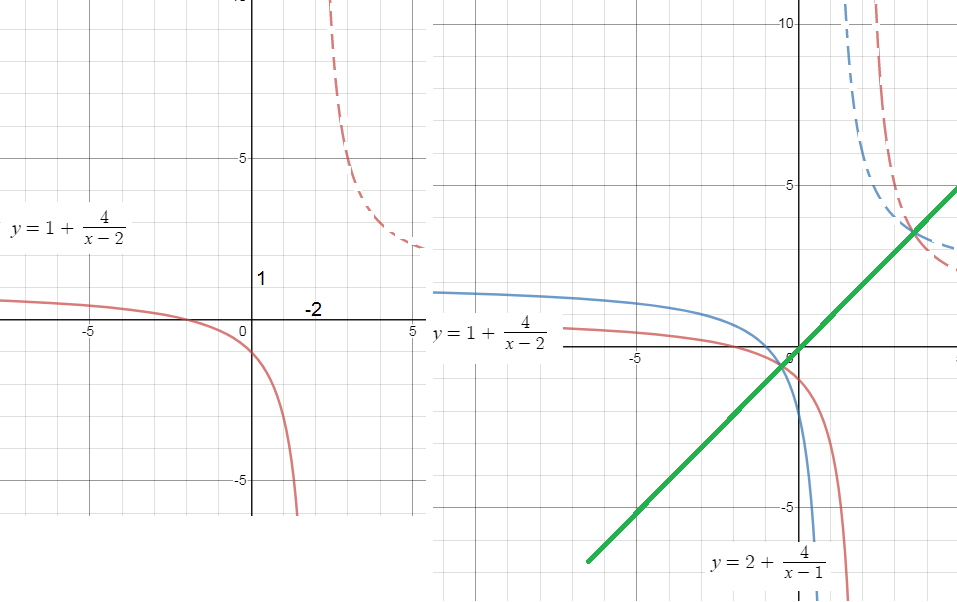
y=1+[m]\frac{4}{x-2}[/m]
x ∈ (- ∞ ;2) ⇒ y ∈ (- ∞;1)
левая ветвь гиперболы.
(см. рис.1)
меняем х и у местами
x=1+[m]\frac{4}{y-2}[/m]
находим как из уравнения y
x-1=[m]\frac{4}{y-2}[/m]
y-2=[m]\frac{4}{x-1}[/m]
y=2+[m]\frac{4}{x-1}[/m] - обратная функция (левая ветвь гиперболы синего цвета)
x ∈ (- ∞;1) и y ∈ (- ∞ ;2)
Графики симметричны относительно у=х - биссектрисы 1 и 3 координатных углов ( рис.2)
б)
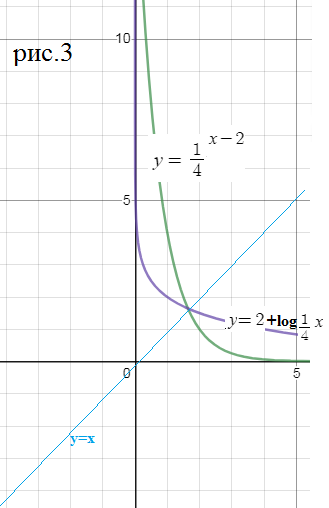
[m]y=(\frac{1}{4})^{x-2}[/m] - график зеленого цвета (см.рис. 3)
Обратная функция:
[m]x=(\frac{1}{4})^{y-2}[/m] ⇒[m]y-2=log_{\frac{1}{4}}x[/m]
[m]y=2+log_{\frac{1}{4}}x[/m] график фиолетового цвета
Графики симметричны относительно биссектрисы у=х- биссектрисы 1 и 3 координатных углов
в)
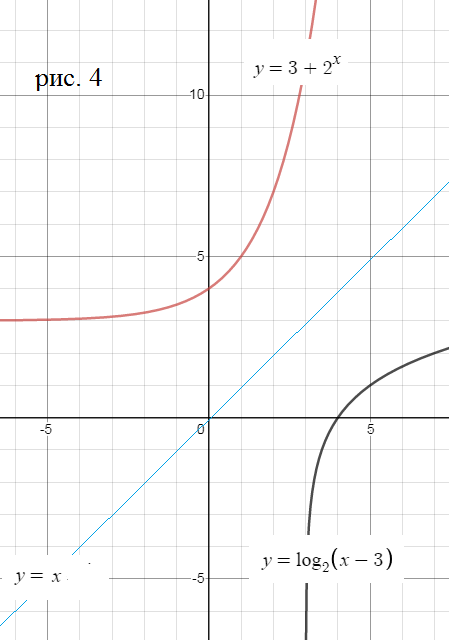
[m]y=log_{2}(x-3)[/m]
Обратная функция:
[m]x=log_{2}(y-3)[/m] ⇒ y-3=2^(x) ⇒ y=2^(x)+3
cм. рис. 4
г)
y=sqrt(16-(x+2)^2)
x ∈ [-6;-2]
Возводим в квадрат
x^2+(y+2)^2=16 - это уравнение окружности с центром (0;-2)
R=4 (cм. рис. 5)
y=sqrt(16-(x+2)^2)
x ∈ [-6;-2]
четвертая часть окружности ( рис. 6)
x ∈ [-6;-2]
y ∈ [0;4]
Обратная функция
x=sqrt(16-(y+2)^2) ⇒
y+2=-sqrt(16-x^2)
y=-2-sqrt(16-x^2)
y∈ [-6;-2]; x ∈ [0;4] - четвертая часть окружности
x^2+(y+2)^2=16
(рис. 7)