Задача 39535 Для заданной функции провести...
Условие
Для заданной функции провести исследование : точки минимума, максимума, точки перегиба; интервалы возрастания , убывания функции ; интервалы выпуклости и вогнутости функции . Построить график функции . На графике функции указать особые точки - точки экстремума , точки перегиба. Построение выполнить схематично.
y=x^3-18x^2+33x+7
Решение
y=x^3-18x^2+33х+7
Область определения (- ∞ ;+ ∞ )
Функция непрерывна, так как является многочленом
y`=3x^2-36x+33
y`=0
3x^2-36x+33=0
x^2-12x+11=0
D=(-12)^2-4*11=144-44=100
x=[m]\frac{12\pm10}{2}[/m]
x_(1)=1; x_(2)=11
Расставляем знак производной ( y`=3x^2-36x+33 - графиком этой функции является парабола, ветви вверх, поэтому на (1;11) производная отрицательна, на двух остальных - положительна):
__+__ (1) __-___ (11) __+__
y`>0 на (- ∞ ;1) и на (11;+ ∞ ), значит функция возрастает
y`< 0 на (1 ;11), значит функция убывает возрастает
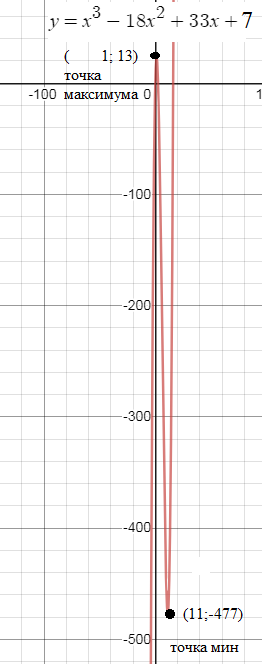
х=1 - точка максимума, производная меняет знак с + на -
у(1)=1^3-18*1^2+33*1+7=[b]13[/b]
х=11 - точка минимума, производная меняет знак с - на +
y(11)=11^3-18*11^2+33*11+7= 11^2*11-18*11^2+3*11^2+7=
=11^2(11-18+3)+7=121*(-4)+7=-484+7=[b]-477[/b]
(просматривается цель заданий - рациональный счет!!! Т.е. уже не первое задание в котором[b] громоздкие вычисления[/b] упрощаются с помощью вынесения за скобки общего множителя)
По этой и причине и график схематический. См. масштаб 1 кл=20
y``=6x-36
y``=0
6x-36=0
x=6- точка перегиба, вторая производная меняет знак с - на +
Функция выпукла вверх на ( - ∞ ;6) и выпукла вниз на (6;+ ∞ )
См. график на рис .