Задача 39084 9^(cosx) + 9^(-cosx) = 10/3 [2Pi;...

slava191

1 сентября 2019 г. в 12:03

9^cosx + 9^–cosx = 10/3

[2π; 7π/2]

sova

1 сентября 2019 г. в 12:47

★

[m]9^{cosx}+\frac{1}{9^{cosx}}=\frac{10}{3}[/m]

Замена переменной:
9^cosx=t
t>0

Уравнение
[m]t+\frac{1}{t}=\frac{10}{3}[/m]

сводится к квадратному:

3t²–10t+3=0
t ≠ 0

D=100–4·3·3=64
[m]t=\frac{10 ± 8}{6}[/m]

t₁=[m]\frac{1}{3}[/m] или t₂=3

Обратно:

9^cosx=[m]\frac{1}{3}[/m];
3^2cosx=3^–1
2cosx=–1

cosx=–1/2
x= ± (2π/3)+2πn, n ∈ Z

или

9^cosx=3
3^2cosx=3¹
2cosx=1

cosx=1/2
x= ± (π/3)+2πn, n ∈ Z

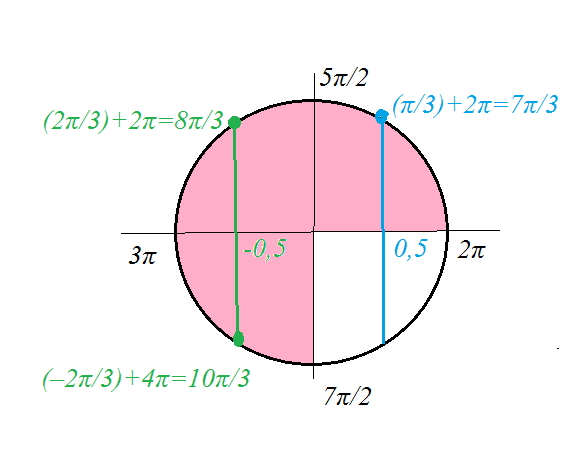
Указанному отрезку принадлежат корни:
х₁=(π/3)+2π=7π/3
х₂= (2π/3)+2π=8π/3
х₃=(–2π/3)+4π=10π/3