Задача 38741 1 Исследуйте ряд на сходимость. 2...
Условие
2 Найдите область сходимости ряда.
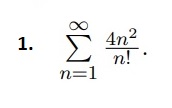
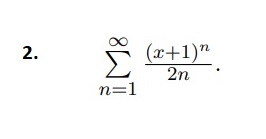
математика ВУЗ
885
Все решения
Применяем признак Даламбера:
lim_(n → ∞ )a_(n+1)/a_(n)=lim_(n→ ∞ )4(n+1)^2*n!/4n^2(n+1)!=
=lim_(n → ∞ )1/(n+1)=0 <1
Сходится
2.
Применяем признак Даламбера к ряду из модулей:
lim_(n → ∞ )a_(n+1)|x|^(n+1)/a_(n)|x|^(n)=
lim_(n→ ∞ )|x+1|^(n+1)2n/2(n+1)*|x+1|^(n)=|x+1|
При |x+1| < 1 ряд сходится. ⇒ x ∈ (-2;0)
При х=-2 получим знакочередующийся числовой ряд∑ (-1)^n/(2n),, он сходится
по признаку Лейбница
При х=0 получим числовой ряд
∑ 1/(2n), который расходится как эквивалентный гармоническому.
О тв е т. [-2;0)
