Задача 38100 Найти точки разрыва, установить их род...

vk230454791

2019-06-12 13:39:27

Найти точки разрыва, установить их род при их наличие,исследовать функцию и построить её график: можете хотя бы первое решить

sova

2019-06-12 14:01:19

a)
y=(-1/3)x^3+x^2

Область определения (- ∞ ;+ ∞ )

Функция непрерывна, так как является многочленом

y`=-x^2+2x

y`=0
-x^2+2x=0
-х*(х-2)=0

x_(1)=0; x_(2)=2

Расставляем знак производной ( y`=-x^2+2x - графиком этой функции является парабола, ветви вниз, поэтому на (0;2) она положительна):

__-__ (0) __+___ (2) __-__

y`<0 на (- ∞ ;0) и на (2;+ ∞ ), значит функция убывает

y`> 0 на (0 ;2), значит функция возрастает

х=2 - точка максимума, производная меняет знак с + на -

у(2)=(-1/3)*2^3+2^2=4-(8/3)=4/3

х=0 - точка минимума, производная меняет знак с - на +

y(0)=0

y``=-2x+2
y``=0
-2x+2=0
x=1- точка перегиба, вторая производная меняет знак с + на -
Функция выпукла вниз на ( (- ∞ ;1) и выпукла вверх на (1;+ ∞ )
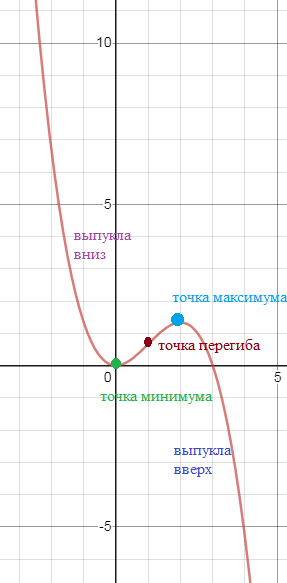
См. график рис. 1