Задача 38098 Вычислить площадь фигуры, ограниченной...
Условие
математика ВУЗ
4044
Решение
★
S= ∫ 40(8–x3/2)dx=
=(8x– x5/2/(5/2))|40=
=(8·4–(2/5)·45/2=32–(64/5)= 96/5 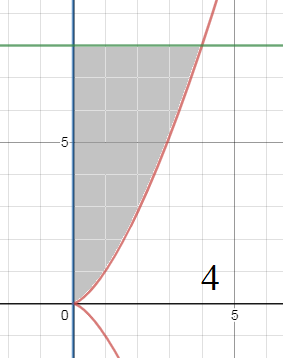
Обсуждения
