Задача 38031 ...
Условие
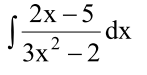
Решение
делим первое слагаемое числителя на знаменатель и второе слагаемое числителя на знаменатель
(2х-5)/(3x^2-2)=(2x)/(3x^2-2) - (5)/(3x^2-2)
Интеграл от суммы равен сумме интегралов:
∫ (2x-5)dx/(3x^2-2)= ∫ 2xdx/(3x^2-2) - ∫ 5dx/(3x^2-2)=
первый интеграл сводим к интегралу ∫ du/u=ln|u|
второй по формуле ∫ du/(u^2-a^2)=(1/(2a))* ln|(u-a)/(u+a) + C
Итак, решение можно записать коротко так:
∫ (2x-5)dx/(3x^2-2)= ∫ 2xdx/(3x^2-2) - ∫ 5dx/(3x^2-2)=
=(1/3) ∫ (6xdx)/(3x^2-2) - 5*∫dx/((sqrt(3)x)^2-2)=
=(1/3) ∫ d(3x^2-2)/(3x^2-2)-(5/sqrt(3)) ∫ d(sqrt(3)x)/((sqrt(3)x)^2-2)=
=(1/3)ln|3x^2-2| -(5/sqrt(3))*(1/(2sqrt(2)))ln|(sqrt(3)x-sqrt(2))/(sqrt(3)x+sqrt(2))| + C=
= [b](1/3)ln|3x^2-2| -(5/(2sqrt(6)))*ln|(sqrt(3)x-sqrt(2))/(sqrt(3)x+sqrt(2))| + C[/b]
