Задача 38018 Найдите длину l дуги кривой линии...
Условие
Все решения
x(t)=acos^4t
y(t)=asin^4t
тогда
sqrt(x)=sqrt(a)cos^2t
sqrt(y)=sqrt(a)sin^2t
Складываем
sqrt(x)+sqrt(y)=sqrt(a)*(cos^2t+sin^2t)
sqrt(x)+sqrt(y)=sqrt(a)
Поэтому применяем формулу:
L= ∫ ^(t_(2))_(t_(1))sqrt [b]([/b] ((x`(t))^2+(y`(t))^2 [b])[/b]dt
x`(t)= 4acos^3t*(cost)`=4acos^3t*(-sint)
y`(t)=4asin^3t*(sint)`=4asin^3t*cost
(x`(t))^2+(y`(t))^2=16a^2*(cos^6t*sin^2t+sin^6t*cos^2t)=
=16a^2*sin^2tcos^2t*(cos^4t+sin^4t)=
формула понижения степени: sin^2x=(1-cos2x)/2;cos^2x=(1+cos2x)/2⇒
sin^4t+cos^4t=(sin^2t)^2+(cos^2t)^2=(2+2cos^2x)/4=(1+cos^2x)/2
=4a^2*(sin2t)^2*(1+cos^22t)/2=2a^2(sin^22t)*(1+cos^22t)
При x=0
t_(1)=π/2
При х=а ⇒ acos^4t=a ⇒ cos^4t=1 ⇒ cos^2t=1;
cost=1
t_(2)=0
∫ ^(0)_(π/2) = [b]-[/b] ∫ ^(π/2)_(0)
L= - ∫ ^(π/2)_(0) sqrt(2)a*sin2t*sqrt(1+cos^22t)dt=
=sqrt(2)a ∫ ^(π/2)_(0)sqrt(1+cos^22t)d(cos2t)/2=
=(sqrt(2)/2)* a* [b]([/b]cos2t+sqrt(1+cos^22t)+ln|cos2t+sqrt(1+cos^22t))/2|) | ^(π/2)_(0)=
=a*(sqrt(2)/4)(0 + +ln|cosπ+sqrt(1+cos^2π))/2|-ln|cos0+sqrt(1+cos^20))/2|=
[b]=a*sqrt(2)ln(sqrt(2)-1)/8- asqrt(2)*ln(sqrt(2)+1)/8[/b] 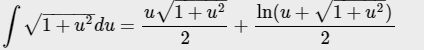
y=0 x=a
l= ∫sqrt(1+y'^2)dx от 0 до a
y'=1- sqrt(a/x)
l= ∫sqrt(2-2*sqrt(a/x)+a/x)dx
