Задача 37959 Решить уравнение: [b]sqrt(8-7x)=-x [/b]...

sova

2019-06-05 12:02:43

Решить уравнение:
[b]sqrt(8-7x)=-x [/b]

Первый способ

Находим ОДЗ.

Квадратный корень нельзя извлечь из отрицательного числа
По определению арифметического квадратного корня - это число неотрицательное.
Поэтому получаем систему неравенств:

{8–7x ≥ 0 ⇒ –7x ≥ –8 ⇒ x ≤ 8/7
{–x ≥ 0 ⇒ x ≤ 0

ОДЗ x ∈ (– ∞ ;0]

Возводим в квадрат
8–7x=(–x)^2
x^2+7x–8=0
D=49–4·(–8)=81
x_(1)=(–7–9)/2=–8; х_(2)=(–7+9).2=1

x_(2)=1 не удовлетворяет ОДЗ
корнем данного уравнения не является

О т в е т. –8

[b]Второй способ.[/b]

Возводим в квадрат и делаем проверку.
8–7x=(–x)^2
x^2+7x–8=0
D=49–4·(–8)=81
x_(1)=(–7–9)/2=–8; х_(2)=(–7+9).2=1

П р о в е р к а.

При х=–8
√8–7·(–8)=–(–8)
√64=8 – верно

При х=1
√8–7·1=–1
√1=–1 – неверно, противоречит определению арифметического квадратного корня

О т в е т. –8


[b]Третий способ[/b]
Графический способ решения.

Строим график функции y=sqrt(8-7x) и график y=-x
Cм. рис.


О т в е т. -8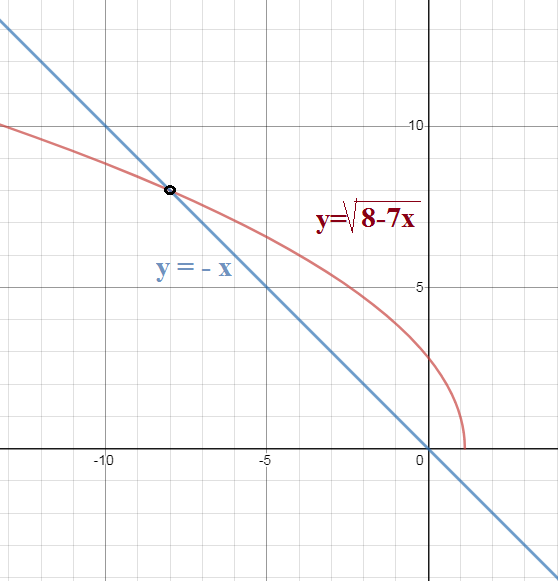

vk397114329

2020-02-21 00:21:20

★

sgrt(8-7x)=-x
Решение:
ОДЗ: -x ≥ 0, x ∈ (- ∞ ;0 )
sgrt(8-7x)+ x=0. Воспользуемся тем , что сумма двух убывающих
функций есть функция убывающая на их общей области определения. поэтому данное уравнение не может иметь более одного корня.
Поэтому подбором находим корень уравнения x=-8
Проверка : sgrt(8+ 56)=8-верно.
Ответ:-8.