Задача 37188 ...
Условие
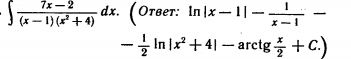
Все решения
Первый множитель в знаменателе должен быть в квадрате.
Очень [b]непочетное это дело [/b]решать задачи с опечатками.....
(7x-2)/((x-1) [b]^2[/b](x^2+4))=A/(x-1)+B/(x-1)^2+ (Mx+N)/(x^2+4)
7х-2=А*(x^2+4)(x-1)+B*(x^2+4) +(Mx+N)*(x-1)^2
7x-2=Ax^3-Ax^2+4Ax-4A+Bx^2+4B+Mx^3-2Mx^2+Mx+Nx^2-2Nx+N
A+M=0
B-A-2M+N=0
4A+M-2N=7
-4A+4B+N=-2
A=-M
B-M+N=0 ⇒ M=B+N
-3M-2N=7 ⇒ -3*(B+N)-2N=7 ⇒ -3B-5N=7
4M+4B+N=-2 ⇒ 4*(B+N)+4B+N=-2 ⇒ 8B+5N=-2
Cкладываем
5B=5
B=1
N=-2
M=-1
A=1
= ∫ dx/(x-1)+ ∫dx/(x-1)^2+ ∫(-x-2)dx/(x^2+4)=
=∫ dx/(x-1)+ ∫dx/(x-1)^2 -∫ (xdx/(x^2+4) -2 ∫dx/(x^2+4)=
=ln|x-1|- (1/(x-1) - (1/2) ∫ d(x^2+4)/(x^2+4) -2*(1/2)* arctg(x/2)=
=ln|x-1|-- (1/(x-1)- (1/2)(ln(x^2+4) - arctg(x/2)+C

