Задача 36638 ...
Условие
1,5 ∫ 0 dx/sqrt(81 + x^4)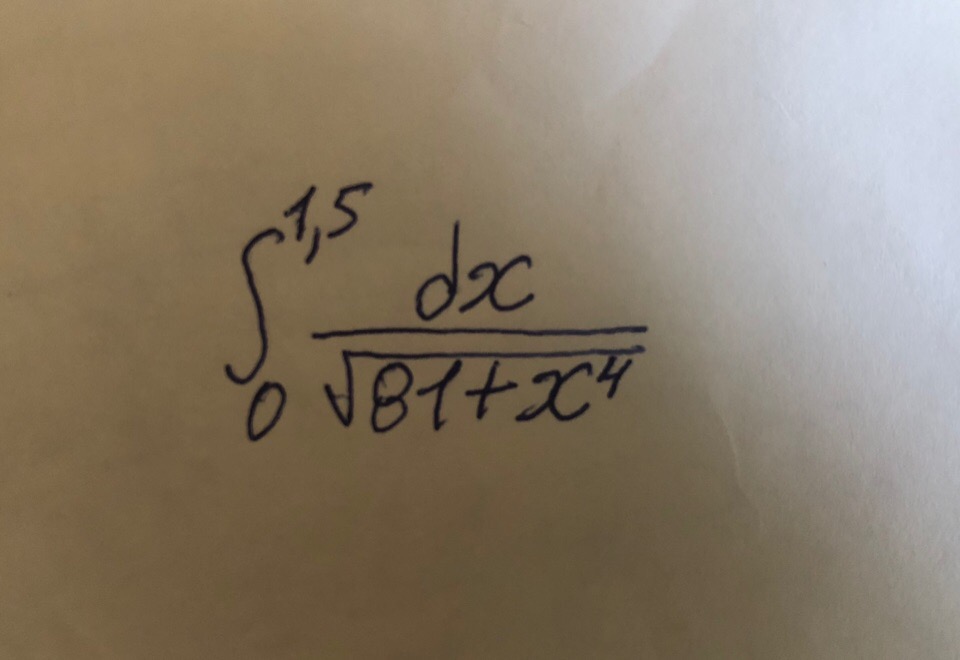
математика ВУЗ
1027
Решение
★
(см. приложение).
sqrt(81+x^4)=sqrt(81*(1+(x^4/81))=9*sqrt(1+(x^4/81))
1/sqrt(81+x^4)=(1/9)*(1+(x^4/81))^(-1/2)/3=
=(1/9)*(1-(1/2)*(x^4/81)+(1/2!)*(-1/2)*((-1/2)-1)*(x^4/81)^2+...
=(1/9)-(1/(18*81))*x^4+(3/72)*(x^8/81^2)+...
(x/3)^4 < 1 ⇒ -3<x<3
∫ ^(1,5)_(0) dx/sqrt(81+x^4)=
= ∫ ^(1,5)_(0) [b]([/b](1/9)-(1/(18*81))*x^4+(3/72)*(x^8/81^2) [b])[/b]dx=
= [b]([/b](1/9)x- (1/1458)*(x^5/20) +(3/(72*81^2))*(x^9/9) [b])[/b]|^(1,5)_(0)=
=считайте...