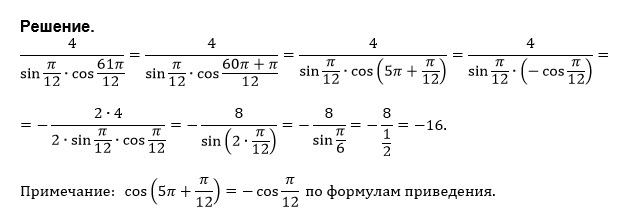Задача 36566 [block]Найдите значение выражения:...

vk505156332

2019-04-29 13:47:32

[block]Найдите значение выражения: (4)/(sin(Pi/12)*cos(61Pi/12))[/block]

sova

2019-04-29 14:14:50

Так как
по формулам приведения:
сos(61π/12)=cos((60π/12) +(π/12))=cos(5π+(π/12))= [b]-cos(π/12)[/b]

и по формуле синуса двойного угла

2*sin(π/12)*cos(π/12)=sin(π/6)= [b]1/2[/b],

то


4/(sin(π/12)·cos(61π/12))= 4/(-sin(π/12)·cos(π/12))=

=-8/(2*sin(π/12)*cos(π/12))=-8/sin(π/6)= -8/(1/2)=-16

О т в е т. [b]-16[/b]