Задача 36125 ...

raffaello

2019-04-20 19:06:26

Решите уравнение sin 2x + 2 cos^2 x + cos 2x = 0.

Найдите корни этого уравнения, принадлежащие отрезку [ -9π/2; -3π ].

sova

2019-04-20 20:04:39

cos2x=cos^2x-sin^2x
sin2x=2sinxcosx

Уравнение принимает вид

sin^2x-2sinxcosx-3cos^2x=0 - однородное второй степени.
Делим на сos^2x ≠ 0

tg^2x-2tgx-3=0
D=4-4*(-3)=16

tgx=-1 или tgx=3
[b]x=(-π/4)+πk, k ∈ Z[/b] или [b]x=arctg3 +πn, n ∈ Z[/b]

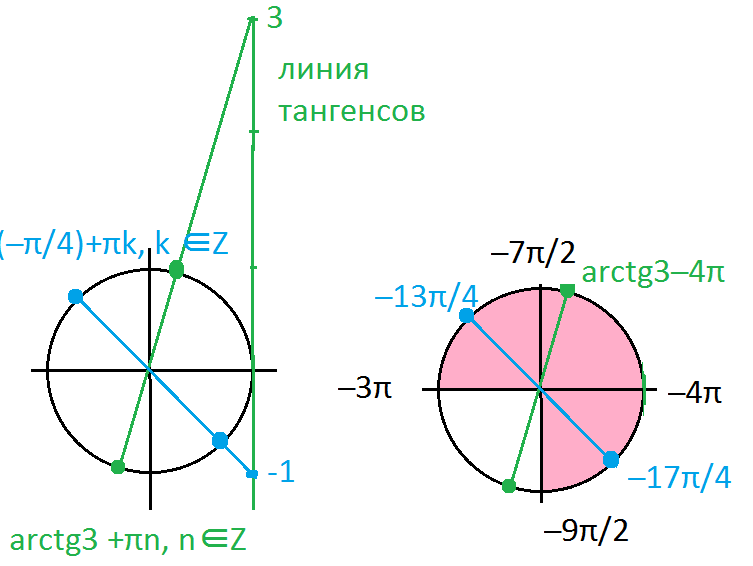
б) Указанному промежутку принадлежат корни
x_(1)=(-π/4)-4π=-17π/4
x_(2)=arctg3-4π
x_(3)=(-π/4)-3π=-13π/4
Cм. рис.