Задача 35521 Используя методы дифференциального...
Условие
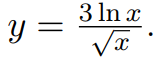
Решение
(0;+∞)
2. Функция не является ни четной, ни нечетной, так как
область определения не является симметричной относительно 0.
3. Точки пересечения с осью Ох
y=0 ⇒ 3lnx=0⇒x=1
(1;0)– точка пересечения и осью Ох
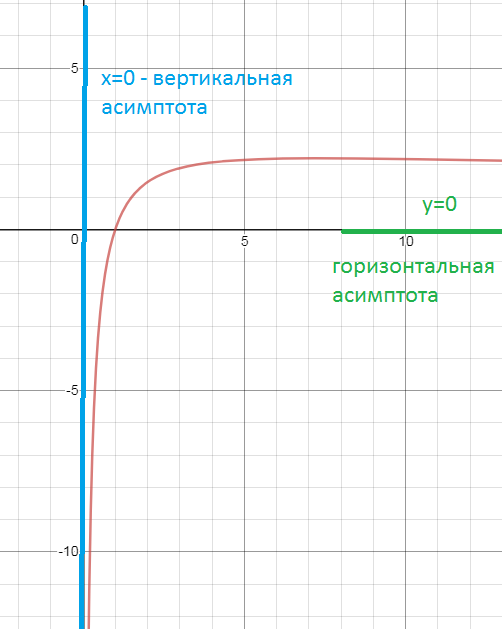
4. Асимптоты
[b]x=0[/b] – правосторонняя вертикальная асимптота
так как
imx→+0(y)= + ∞
Горизонтальная асимптота:
[b]y=0[/b]
так как
limx→∞(3lnx)/sqrt(x)= ∞/∞
=применяем правило Лопиталя:
=limx→∞(3lnx)`/(sqrt(x))`=limx→∞(3/x)/(1/(2sqrt(x)))=6/sqrt(x)=0
(очень медленно, но стремится к 0 на +бесконечности)
Наклонной асимптоты нет:
k=limx→∞f(x)/x=limx→∞(3lnx)/(х*sqrt(x)= ∞/∞
=применяем правило Лопиталя:
=limx→∞(3lnx)`/(x*sqrt(x))`=limx→∞(3/x)/(3/2)sqrt(x)=
=limx→∞(3/(x*sqrt(x))=0
5.Интервалы монотонности и экстремумы
y`=3*(lnx)`*sqrt(x)-(sqrt(x))`*lnx)/(sqrt(x))^2
y`=3(2-lnx)/(2x)
lnx=2
x=e^(2)
Расставляем знак производной:
(0) _+__ (e^(2)) __-__
x=e^(2) - точка максимума.
y`>0 при 0<x<e^(2)
Функция возрастает на (0;e^(2))
y`<0 при x>e^(2)
Функция убывает на (e^(2);+ ∞)
6.
Интервалы выпуклости, точки перегиба
y``=(3/2)*((2-lnx)`·(x) – (x)`·(2–lnx))/(x)^2
y``=(3/2)*((-1-2+lnx)/x^2)
y``=(-1-2+lnx)/x^2
y``=0
lnx=3
x=e^(3) - точка перегиба, производная меняет знак с - на +
y`` < 0 на (0;e^(3))
Кривая выпукла вверх на (0;e^(3))
y``>0 на (e^2;+ ∞)
Кривая выпукла вниз на (e^2;+ ∞)