Задача 35457 (x + ycos y/x )dx - xcos y/x dy = 0...
Условие
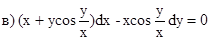
математика ВУЗ
884
Решение
★
Делим на х
(1+(y/x)*cos(y/x))dx=cos(y/x) dy
Однородное уравнение 1 порядка.
Решают заменой:
y/x=u
y=xu
dy=xdu+udx
(1+u*cosu)dx=cosu*(xdu+udx)
(1+u*cosu-u*cosu)dx=x*cosudu
dx/x=cosudu
∫dx/x= ∫ cosudu
ln|x|+lnC=sinu
ln|x|+lnC=sin(y/x)
e^(sin(y/x))=Cx - о т в е т
