Задача 35329 ...
Условие
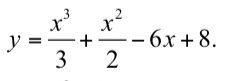
Решение
1.область определения функции D(y)=(- ∞ ; + ∞ )
2. Область изменения функции E(y) =(-∞ ; + ∞ )
см. рис.
3. Чётность или нечётность функции
f(-x)=((-x)^3/3) + ((-x)^2/2) - 6*(-х)+8=(-x^3/3)+(x^2/2)+6x+8
f(-x)≠ f(x)
f(-x) ≠ -f(x)
Функция не является ни чётной, ни нечётной
Функция непрерывна на области определения, потому что это многочлен
Поведение функции на бесконечности
lim_(x→+∞) y =+∞
lim_(x→ - ∞)y = -∞
Исследование функции с помощью производной
y`=(3x^2/3)+(2x/2)-6
y`=x^2+x-6
y`=0
x^2+x-6=0
D=1-4*(-6)=25
x_(1)=(-1-5)/2=-3 или x=(-1+5)/2=2
Знак производной
_+__ (-3) __-__(2) ___+_
Возрастает на (- ∞ ; -3) и на (2; + ∞ )
Убывает на (-3; 2)
х= -3 - точка максимума y(-3)=(-3)^3/3+(-3)^2/2-6*(-3)+8=21,5
x=2 - точка минимума y(2)=(2)^3/3+(2)^2/2-6*(2)+8=2/3
y``=2x+1
y``=0
x=-1/2 - точка перегиба, вторая производная при переходе через точку меняет знак с - на +
y``<0 на (- ∞ ; -1/2), кривая выпукла вниз
y``>0 на (-1/2; + ∞ ) кривая выпукла вверх
См. рис.