Задача 35295 Помогите пожалуйста...
Условие

Решение


Все решения
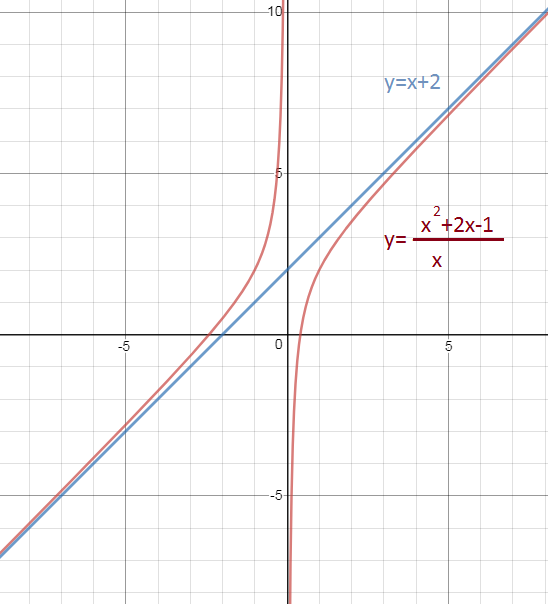
1.область определения функции D(y)=(- ∞ ;0) U(0; + ∞ )
2. Область изменения функции E(y) =(-∞ ; + ∞ )
см. рис.
3. Чётность или нечётность функции
f(-x)=((-x)^2+2*(-х)-1)/((-x))=(x^2-2х-1)/(-x)
f(-x)≠ f(x)
f(-x) ≠ -f(x)
функция не является ни чётной ни нечётной
4.периодичность - непериодическая
5.нули функции
y=0
x^2+2x-1=0
D=4-4*(-1)=8
x_(1)=(-2-2sqrt(2))/2=-1-sqrt(2); x_(2)=(-2+2sqrt(2))/2=-1+sqrt(2);
6.интервалы знака постоянства
_-__(-1-sqrt(2)) __+__ (0) __-__( -1+sqrt(2)) ____+__
y > 0 при x<-1-sqrt(2) и 0 <x <-1+sqrt(2)
y < 0 при -1-sqrt(2) < x < 0 и х > -1+sqrt(2)
Исследование с помощью теории пределов
7.непрерывность функции
непрерывна на области определения как частное непрерывных функций
8.поведение функции на бесконечности
lim_(x→+∞) f(x) =+∞
lim_(x→ - ∞)f(x) = -∞
9.асимптоты граф. функции
[b]x=0 - вертикальная асимптота[/b], так как оба [b] односторонних предела бесконечны:[/b]
lim_(x→ - 0) f(x) =+∞
lim_(x→ + 0) f(x) =+∞
k=lim_(x→ ∞)f(x)/x=lim_(x→ ∞)(x^2+2x-1)/(x^2)=1
b=lim_(x→ ∞)(f(x)-kx)=lim_(x→ ∞)(((x^2+2х-1)/(x))-x)=lim_(x→ ∞)(2x-1)/x=2
y=x + 2 - [b]наклонная асимптота[/b]
3.) исследовать с помощью производной
y`=((x^2+2x-1)`*x-(x)`*(x^2+2x-1))/(x)^2
y`=(x^2+1)/(x^2) > 0
Возрастает на (-∞ ; 0) и на (0; + ∞ )
4) y``=(x^2+1)`*x^2-(x^2)`*(x^2+1)/x^4=(2x*x^2-2x*(x^2+1))/x^4=-2x/x^4=-2/x^3
y``>0 на (-∞ ; 0)
Функция выпукла вниз
y``< 0 на (0;+∞ )
Функция выпукла вверх
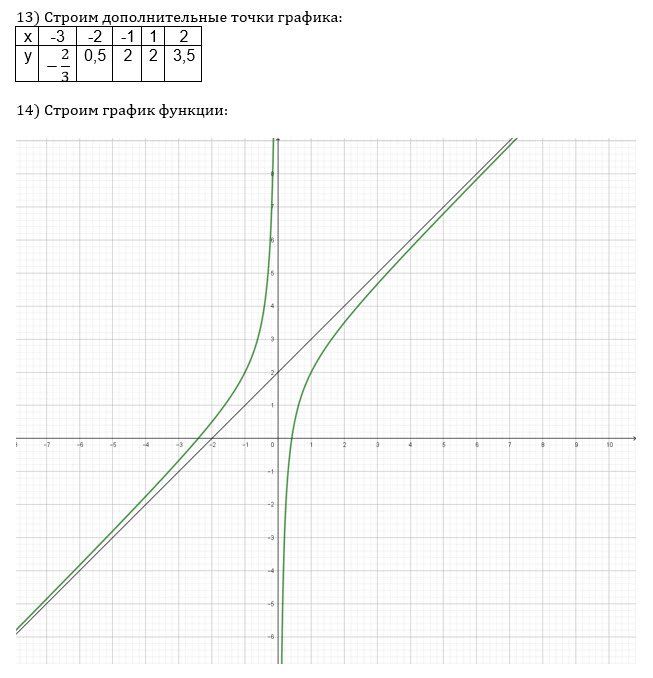
См. рис.