Задача 35271 ...

nastyaaaa

2 апреля 2019 г. в 20:53

4. Вычислите площадь фигуры, ограниченной линиями:

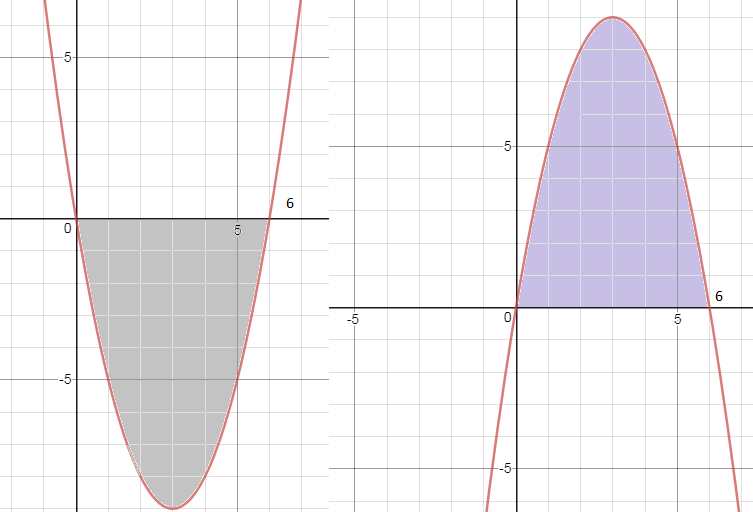
y = x² – 6x
y = 0

y = x² + 1
y = 5

sova

2 апреля 2019 г. в 21:30

★

1. Криволинейной трапецией называется фигура, ограниченная кривой у=f(x), f(x)≥ 0, прямыми x=a; x=b; a<b и осью Ох

Тогда площадь такой трапеции и есть интеграл по отрезку [a;b]
от функции f(x)

В остальных случаях существуют правила.

Так как

y=x²–6x и прямая y=0 ограничивают фигуру, которая расположена ниже оси Ох, то считают площадь фигуры,
ограниченной кривой y=–x²+6x

см. рис. Площади одинаковы.

S= ∫ ⁶₀|x²–6x|dx=∫ ⁶₀(–x²+6x)dx=

=((–x³/3)+(6x²/2))|⁶₀=–(6³/3)+3·6²=

=–72+108= 36

2.
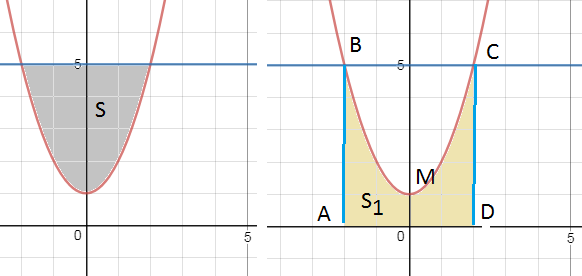
S=S_{прямоугольника ABCD}– S_{1 криволинейной трапеции ABMCD}=

=4·5– ∫ ²_–2(x²+1)dx= 20– ((x³/3)+x)|²_–2=

=20–((8/3)+2)+((–8/3)–2)=

=20–(28/3)= 32/3