Задача 35012 По чертежу определить формулу для...
Условие
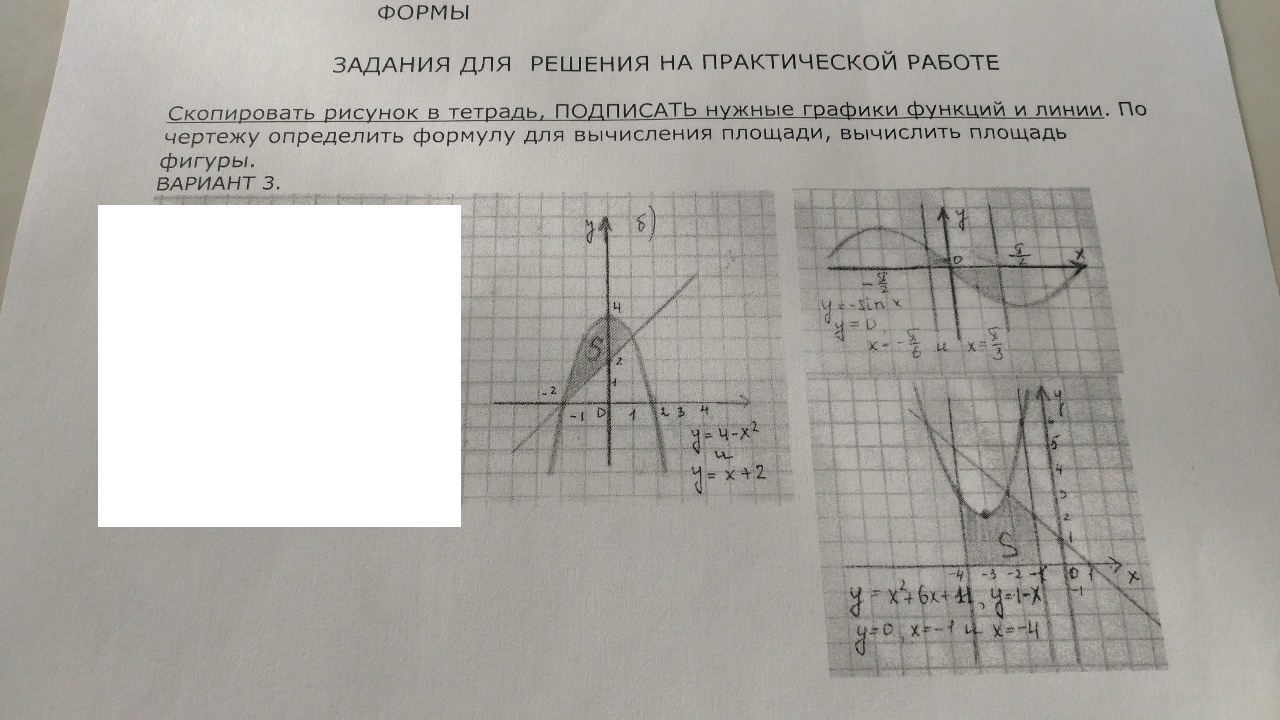
математика ВУЗ
815
Решение
★
S= ∫ ^(1)_(-2)((4-x^2)-(x+2))dx= ∫ ^(1)_(-2)(4-x^2-x-2)dx= ∫^(1)_(-2)(2-x^2-x)dx=
=(2x-(x^3/3)-(x^2/2))|^(1)_(-2)=(2-(1/3)-(1/2)) - (4-(-8/3)-(4/2))=
2)
S= ∫ ^(π/3)_(-π/6) |-sinx|dx = ∫ ^(0)_(-π/6)(-sinx)dx+ ∫ ^(π/3)_(0)sinxdx=
=cosx|^(0)_(-π/6) - cosx| ^(π/3)_(0)=cos0-cos(-π/6)-cosπ/3+cos0=1-(1/2)-sqrt(3)/2+1=
=
3)
S= ∫^(-2) _(-4)(x^2+6x+11)dx+ ∫^(-1)_(-2)(1-x)dx=
=((x^3/3)+(6x^2/2)+11x)|^(-2) _(-4) + (x-(x^2/2))|^(-1)_(-2)=
=(-8/3)+3*4-22 - (-64/3)-3*(16)-11*(-4) (-1-(1/2))-(-2-(4/2))=
