Задача 34912 Вычислить несобственный интеграл или...
Условие
расходимость.
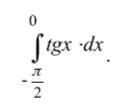
математика
1148
Решение
★
∫^(0)_(π/2)tgxdx= ∫^(0)_(π/2)sinxdx/cosx= - ∫^(0)_(π/2)d(cosx)/cosx=
=(ln|cosx|)|^(0)_(π/2)=ln|cos0|- ln |cos(π/2)|=ln1 - ln 0=0-(- ∞ )=+ ∞
Расходится.
