Задача 34911 Вычислить интегралы. ...
Условие
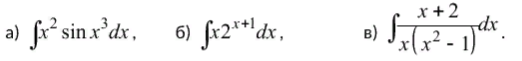
Решение
∫ sin [b]u[/b]d [b]u[/b]=-cosu+C
u=x^3
du=3x^2dx
x^2dx=(1/3)du
∫ x^2*sin^3xdx=(1/3) ∫ sinudu=(1/3)*(-cosu)+C= [b]-(1/3)cosx^3+C[/b]
б)
2^(x+1)=2^(x)*2^(1)=2*2^(x)
интегрируем по частям:
u=x ⇒ du=dx
dv=2^(x)dx ⇒ v= ∫ 2^(x)dx=2^(x)/ln2 + C
∫ udv=u*v- ∫ v*du
получаем
∫ x*2^(x+1)dx=2* ∫ x* [b]2^(x)dx[/b]= 2*(x*2^(x)/ln2)-2* ∫ 2^(x)dx/ln2=
= 2*(x*2^(x)/ln2)- (2/ln2) *(2^(x)/ln2) + C=
= [b](x*2^(x+1)/ln2) - (2^(x+1)/(ln^22) + C[/b]
в) см. интегрирование рациональных дробей.
раскладываем знаменатель на множители, а дробь на простейшие:
(x+2)/(x*(x-1)(x+1)) = (A/x)+(B/(x-1))+ (D/(x+1))
[b]x+2= A*(x-1)*(x+1) + B*x*(x+1) + D*x*(x-1)[/b]
Применяем метод частных значений.
Если левая и правая части выражения с переменной равны, то они равны и при одном и том же значении переменной:
при х=0
2=-А ⇒ [b]A= - 2[/b]
при х=1
3=2B ⇒ [b] B=3/2[/b]
при х=-1
1=2D ⇒ [b]D=1/2[/b]
О т в е т. -2 ∫ dx/x +(3/2) ∫ dx/(x-1)+(1/2) ∫ dx/(x+1)=
= [b]-2ln|x|+(3/2)ln|x-1|+(1/2)ln|x+1| + C[/b]
