Задача 34859 Построить график функции y = f (x) ,...
Условие
функции.
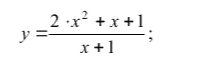
Решение
(- ∞ ;-1) U(-1;+ ∞ )
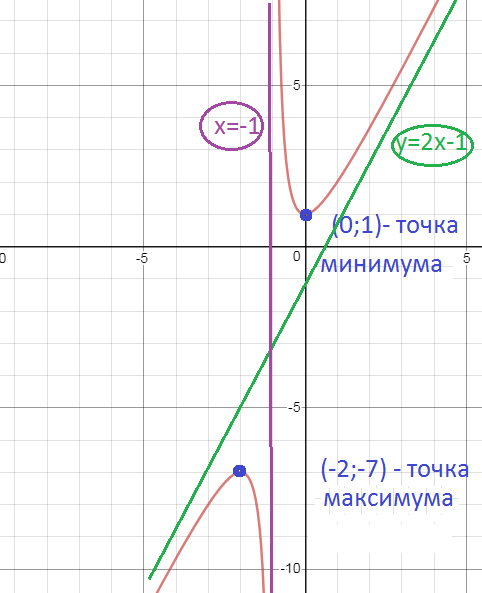
[b]x=-1 - вертикальная асимптота[/b]
так как
lim_(x→-1)f(x)= ∞
Горизонтальной асимптоты нет
lim_(x→ ∞)f(x)= ∞
Есть [b]наклонная асимптота[/b]
k=lim_(x→ ∞)f(x)/x= lim_(x→ ∞) (2x^2+x+1)/(x*(x+1))=2
b=lim_(x→ ∞)(f(x)-kx)=lim_(x→ ∞) ((2x^2+x+1)/(x+1) - 2x)=
=lim_(x→ ∞) ((2x^2+x+1-2x^2-2x)/(x+1)==lim_(x→ ∞) (-x+1)/(x+1)=-1
[b]y=2x-1[/b]
[b]Исследование функции с помощью первой производной[/b]
y`=((2x^2+x+1)`*(x+1)-(x+1)`*(2x^2+x+1))/(x+1)^2
y`=((4x+1)*(x+1)-(2x^2+x+1))/(x+1)^2
y`=(2x^2+4x)/(x+1)^2
y`=0
2x^2+4x=0
2x*(x+2)=0
x=0 или x=-2
Отмечаем точки на области определения:
_+__ (-2) _-__ (-1) __-_ (0) __+__
y`>0 функция возрастает на (- ∞ ;-2) U(0;+ ∞ )
y`< 0 функция убывает на (-2;-1) U(-1;0 )
х=-2 - точка максимума y(-2)=-7
х=0 - точка минимума y(0)=1
[b]Исследование функции с помощью второй производной[/b]
y``=((4x+4)*(x+1)^2-2(x+1)*(2x^2+4))/(x+1)^4
y``=((4x+4)*(x+1)-2*(2x^2+4))/(x+1)^3
y``=4/(x+1)^3
y``>0 на (-1;+ ∞ )
кривая выпукла вниз
y``<0 на (- ∞;-1 )
кривая выпукла вверх
точек перегиба нет