Задача 34804 решим по схеме которая дана на фото 1)...
Условие
1) провести полное исследование указанных функций и построить их график
y=x ln x
Решение
2. Не является ни четной, ни нечетной потому что область определения не является симметричной относительно нуля.
3.Непериодическая.
Ни при каком Т не выполняется равенство f(x+T)=f(x) для любого х из D(y)
4.Непрерывна на области определения как произведение непрерывных функций.
5.
lim_(x→+ ∞)= + ∞
Горизонтальной асимптоты нет.
lim_(x→+ 0)x*lnx=
(0* ∞)- неопределенность сводим к неопределенности ∞ / ∞
=lim_(x→+ 0)lnx/(1/x)=( ∞ / ∞ )
применяем правило Лопиталя
=lim_(x→+ 0)(lnx)`/(1/x)`=lim_(x→+ 0)(1/x)/(-1/x^2)=lim_(x→+ 0)l(-x)=0
Вертикальной асимптоты нет.
k=lim_(x→+ 0)f(x)/x=lim_(x→+ 0)lnx=- ∞
Наклонной асимптоты нет
y`=(x)`*lnx+x*(lnx)`=1*lnx+ (x) *(1/x)=lnx+1
y`=0
lnx+1 =0
x=e^(-1)
Производная при переходе через точку меняет знак - на +
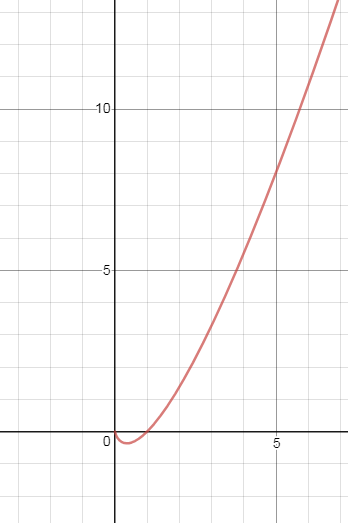
x=e^(-1) - точка минимума.
[b]y(e^(-1))[/b]=e^(-1)*ln(e^(-1)) [b]=-1/e[/b]
Наименьшее значение функции, от него и начинаем считать множество изменений
функции
Функция убывает на (0;e^(-1)) и возрастает на (e^(-1);+ ∞ )
y``=(lnx+1)`=1/x
y``>0 при любом х из области определения, значит функция выпукла вниз
Множество изменений функции
[1/e; + ∞ )