Задача 34778 Помогите пожалуйста !...
Условие
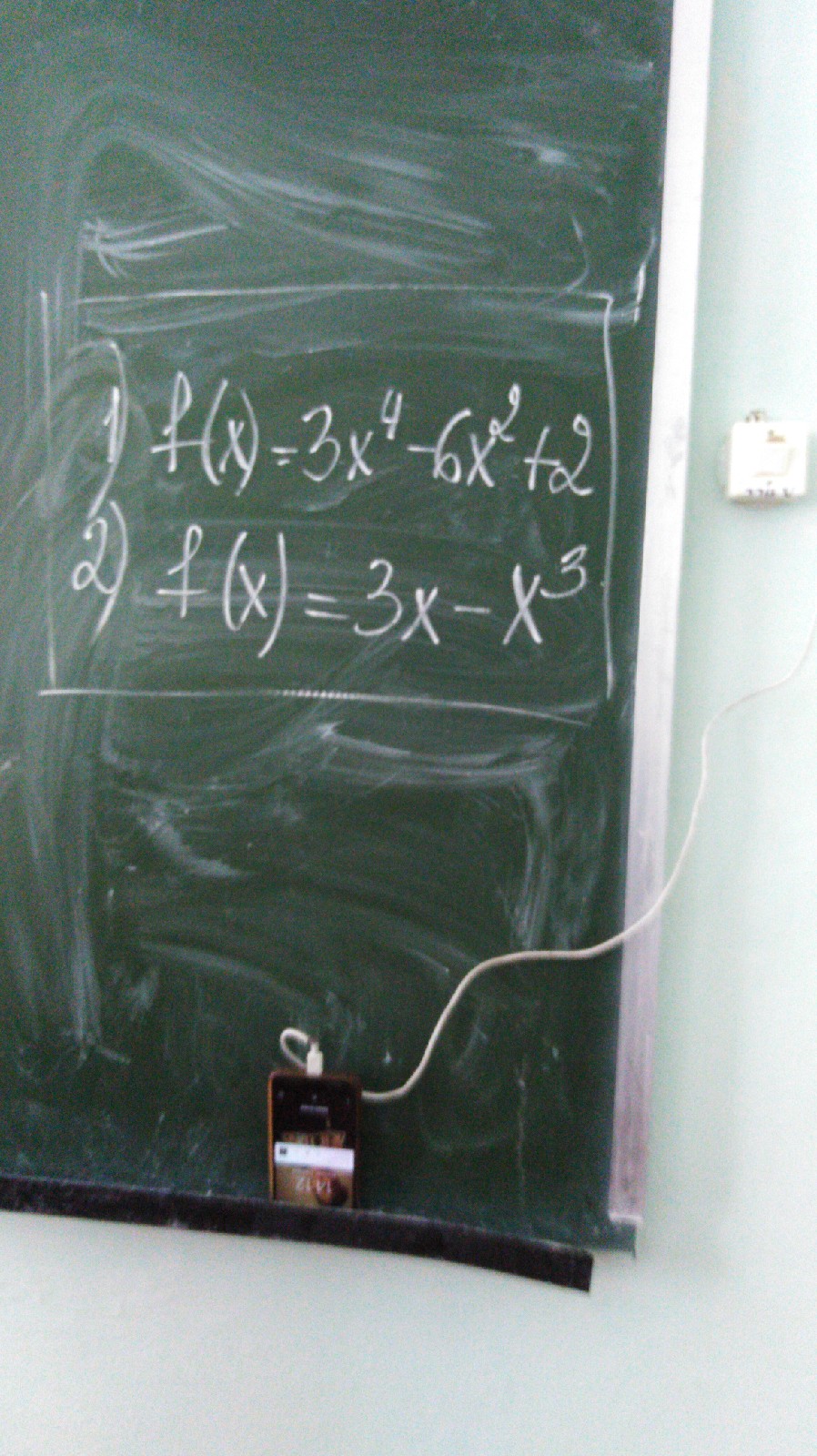
Все решения
f`(x)=12x^3-12x
f`(x)=0
12x^3-12x=0
12х*(x^2-1)=0
x=0 или х= ± 1
Знак производной
_-_ (-1) __+_ (0) _-__ (1) __+__
y`< 0 на (- ∞; -1) и на (0;1)
значит функция убывает на (- ∞; -1) и на (0;1)
y`>0 на (-1;0) и на (1;+ ∞)
значит функция возрастает на (-1;0) и на (1;+ ∞)
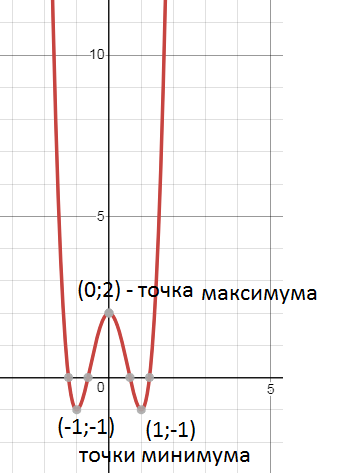
x=-1 и х=1 - точки минимума, производная меняет знак с - на +
х=0 - точка максимума, производная меняет знак с + на -
см. рис.1
2)
f`(x)=3-3x^2
f`(x)=0
3-3x^2=0
3*(1-x^2)=0
x= х= ± 1
Знак производной
_-_ (-1) __+__ (1) __-__
y`< 0 на (- ∞; -1) и на (1;+ ∞)
значит функция убывает на (- ∞; -1) и на (1;+ ∞)
y`>0 на (-1;1)
значит функция возрастает на (-1;1)
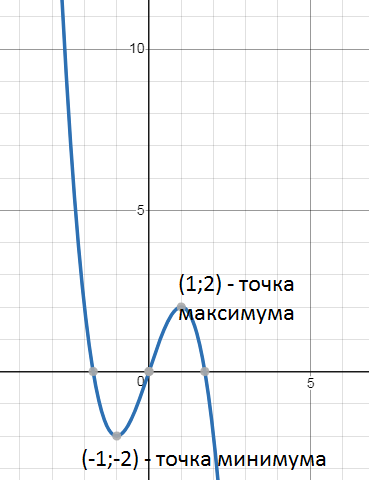
x=-1 - точка минимума, производная меняет знак с - на +
х=1 - точка максимума, производная меняет знак с + на -
см. рис.2