Задача 34578 Полное исследование функции , все ...
Условие

Решение
Область определения
(- ∞ :+ ∞ )
y`=x^2+(x/3)-6
y`=0
x^2+(x/3)-6=0
3x^2+x-18=0
D=1-4*3*(-18)=217
x_(1)=(-1-sqrt(217))/6 или х_(2)=(-1+sqrt(217))/6
y`=x^2+(x/3)-6 - квадратичная функция, график парабола, ветви вверх.
отрицательна между x_(1) и х_(1)
Значит, на ((-1-sqrt(217))/6 ;(-1+sqrt(217))/6) функция убывает,
на (- ∞ ; (-1-sqrt(217))/6 ) и на ((-1+sqrt(217))/6; + ∞ ) функция возрастает
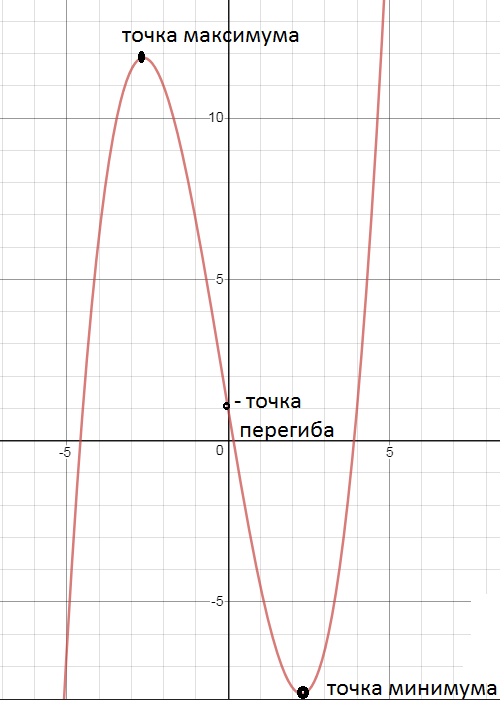
x=(-1-sqrt(217))/6 - точка максимума
х=(-1+sqrt(217))/6 - точка минимума
y``=2x+ (1/3)
y``=0
2x+(1/3)=0
2x=-1/3
x=-1/6
y`` < 0 на (- ∞;-1/6)
функция выпукла вверх
y`` >0 на (-1/6;+ ∞)
функция выпукла вниз
x=-1/6 - точка перегиба.
График см. на рис.
3.2
Область определения
(- ∞ ;-1)U(-1;+ ∞ )
x=-1 - вертикальная асимптота
так как
lim_(x→-1-0)f(x)= -∞
lim_(x→-1+0)f(x)= +∞
Горизонтальной асимптоты нет
lim_(x→+∞)f(x)=+∞
lim_(x→-∞)f(x)=-∞
Наклонная асимптота:
k=lim_(x→∞)f(x)/x=1
b=lim_(x→∞)(f(x)-x)=-8
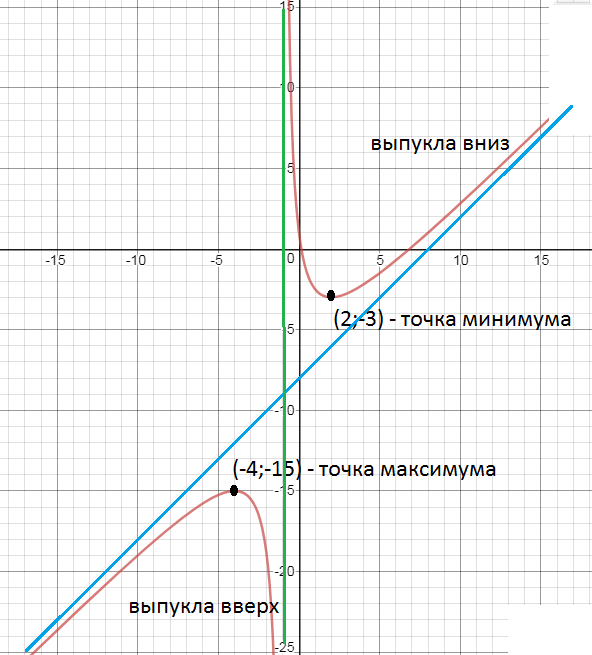
y=x-8 - наклонная асимптота
y`=((x^2-7x+1)`*(x+1)-(x^2-7x+1)*(x+1)`)/(x+1)^2
y`=((2x-7)*(x+1)-x^2+7x-1)/(x+1)^2
y`=(2x^2-7x+2x-7-x^2+7x-1)/(x+1)^2
y`=(x^2+2x-8)/(x+1)^2
y`=0
x^2+2x-8=0
D=2-4*(-8)=36
x_(1)=(-2-6)/2=-4 или х_(2)=(-2+6)/2=2
знак y` зависит от знака числителя, знаменатель в квадрате и значит положителен)
в числителе производной квадратичная функция, график парабола, ветви вверх.
отрицательна между (-4) и 2
Значит, на (-4 ; -1)и на (-1;2) функция убывает,
на (- ∞ ; -4) и на (2/6; + ∞ ) функция возрастает
x=-4 - точка максимума
х=2 - точка минимума
y``=(2x+2)*(x+1)^2-2(x+1)*(x^2+2x-8)/(х+1)^4
y``=(x+1)((2x+2)*(x+1)-2x^2-4x+16)/(x+1)^4
y``=18/(x+1)^3
y``<0 на (- ∞; -1)
кривая выпукла вверх
y``<0 на (-1;+ ∞)
кривая выпукла вниз
Точек перегиба нет.