Задача 34225 Найдите все значения a, при каждом из...
Условие
system{(xy^2-xy-5y+5)/sqrt(5-y) = 0; y=ax}
имеет ровно три различных решения.
Решение
ОДЗ:
5-y>0
y<5
Дробь равна 0, когда числитель равен 0, а знаменатель отличен от нуля
{xy^2-xy-5y+5=0
{y ≠ 5
(xy^2-xy)-(5y-5)=0
xy(y-1)-5(y-1)=0
(y-1)(xy-5)=0
y-1=0 или xy - 5=0
y=1 или xy=5
Геометрически первое уравнение означает объединение двух линий:
прямой y=1
и
гиперболы
y=5/x
При a> 0 прямая y=ax пересекается с гиперболой в двух точках
Прямая y=ax пересекается с прямой y=1 при всех a ≠ 0
Но если прямая y=ax через точку В (5;1) - общую точку
прямой y=1 и гиперболы xy=5, то получим только [b]два решения![/b]
Осталось иcключить значение a, при котором y=1
⇒
1=a*5 ⇒ a=1/5
и исключить значение a, при котором y=5 ( см. ОДЗ y ≠5)
5=a*1
a=5
и исключить значение a, при котором y> 5 ( см. ОДЗ: y < 5)
⇒ a > 5
О т в е т. (0;1/5)U(1/5;5) 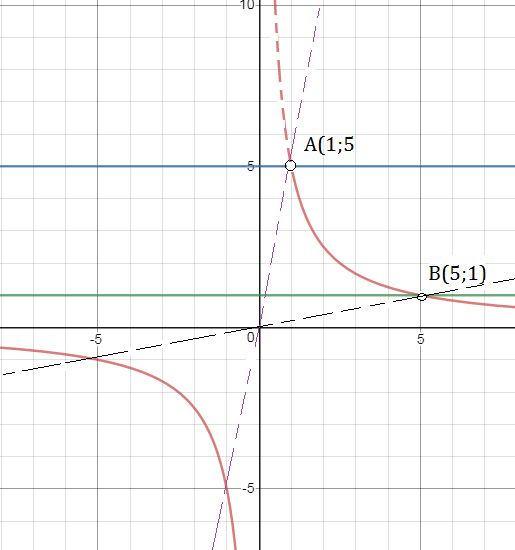
Все решения