Задача 34189 а) Решите уравнение 3-2cos^2x+3sin(x-Pi)...

vk295929291

2019-03-04 22:06:29

а) Решите уравнение 3-2cos^2x+3sin(x-Pi) = 0

б) Найдите корни этого уравнения, принадлежащие промежутку [7Pi/2; 11Pi/2)

sova

2019-03-04 22:59:57

★

По свойству нечетности синуса:
sin(x-π)=-sin(π-x)

По формулам приведения
sin(π-x)=sinx

sin(x-π)=-sinx

Так как
cos^2x=1-sin^2x

Уравнение принимает вид:
1+2sin^2x-3sinx=0

2sin^2x-3sinx+1=0
D=9-4*2*1=1

[b]sinx=1/2 [/b]⇒ x=(-1)^(k)*(π/6)+πk, k ∈ Z

[b]sinx=1 [/b] ⇒ x=(π/2)+2πn, n ∈ Z

О т в е т.
а) (-1)^(k)*(π/6)+πk, k ∈ Z; (π/2)+2πn, n ∈ Z
б)
x=(-1)^(k)*(π/6)+πk, k ∈ Z
удобно записать в виде серии двух ответов:
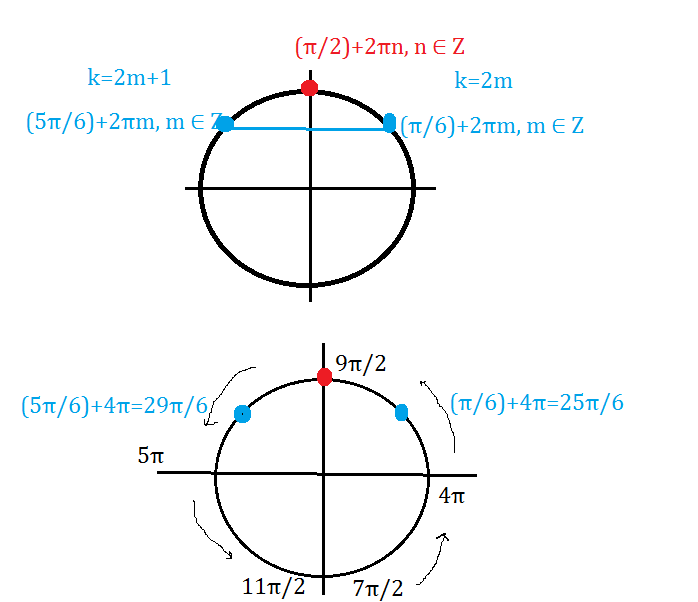
при k=2m получим x=(π/6)+2πm, m ∈ Z
при k=2m+1 получим x=(-π/6)+π+2πm=(5π/6)+2πm, m ∈ Z

Тогда корни, принадлежащие указанному отрезку:
х_(1)=(π/6)+4π=25π/6;
х_(2)=(5π/6)+4π=29π/6;
х_(3)=(π/2)+4π=(9π/2)