Задача 33895 Найти и изобразить на чертеже область...

help

2019-02-25 18:13:55

Найти и изобразить на чертеже область определения функций

а) z=sqrt(3-x^2-y^2)

б) z=ln(4+4x-y^2)

sova

2019-02-25 18:48:58

★

1а)
D(z)={(x;y)|3-x^2-y^2 ≥ 0}
3-x^2-y^2 ≥ 0 ⇒ x^2+y^2 ≤ 3 - внутрення часть круга вместе с границей.
Центр круга в точке (0;0)
R=sqrt(3)

2б)
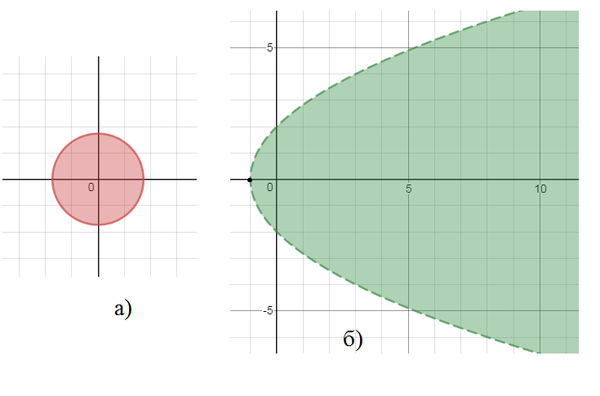
D(z)={(x;y)|4+4х-y^2> 0}
4+4х-y^2> 0 ⇒4(x+1)>y^2 - внутренняя часть параболы
4(х+1)=y^2 c центром (-1;0) ветви в направлении оси ОХ,
граница пунктирной линией