Задача 33889 а) Решить уравнение:...

vk505156332

2019-02-25 15:33:49

а) Решить уравнение: (sin(Pi-x))/(2sin^2(x/2)) = 2cos^2(x/2)

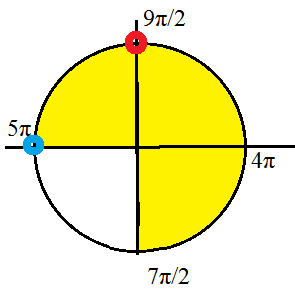
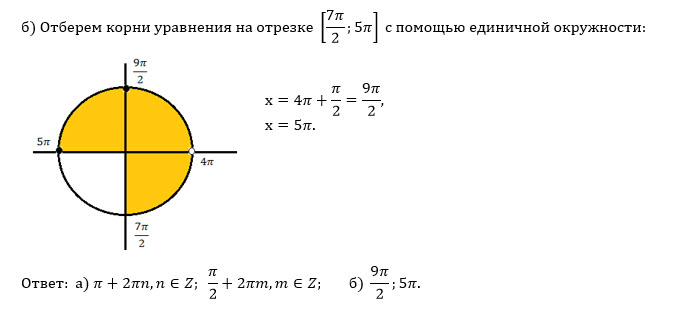
б) Сделать отбор корней на отрезке [7Pi/2;5Pi]

sova

2019-02-25 15:44:46

По формулам приведения
sin(π-x)=sinx

По формулам двойного угла:
2sin^2(x/2)=1-cosx
2cos^2(x/2)=1+cosx

Уравнение:

sinx/(1-cosx) = 1+cosx

(sinx-(1+cosx)*(1-cosx))/(1-cosx)=0

(sinx-(1-cos^2x))/(1-cosx)=0

(sinx - sin^2x)/(1-cosx)=0

{sinx-sin^2x=0
{1-cosx ≠ 0 ⇒ cosx ≠ 1 ⇒ x ≠ 2πm, m ∈ Z

sinx-sin^2x=0
sin*(1-sinx)=0

[b]sinx= 0[/b] ⇒ x=πk, k ∈ Z

Условию x ≠ 2πm, m ∈ Z не удовлетворяют корни при k=2m,

при k=2m+1 корни являются корнями данного уравнения и их
можно записать так :

x=π*(2m+1), m ∈ Z

[b] 1-sinx=0[/b] ⇒ sinx=1 ⇒ x=(π/2)+2πn, n ∈ Z

О т в е т. x=π*(2m+1), m ∈ Z; x=(π/2)+2πn, n ∈ Z

Отрезку [7π/2; 5π]

принадлежат корни

x=5π; x=9π/2