Задача 33884 а) Решите уравнение...

vk505156332

2019-02-25 13:31:52

а) Решите уравнение 2/(tg^2x+1)=3sin(3Pi+2x).

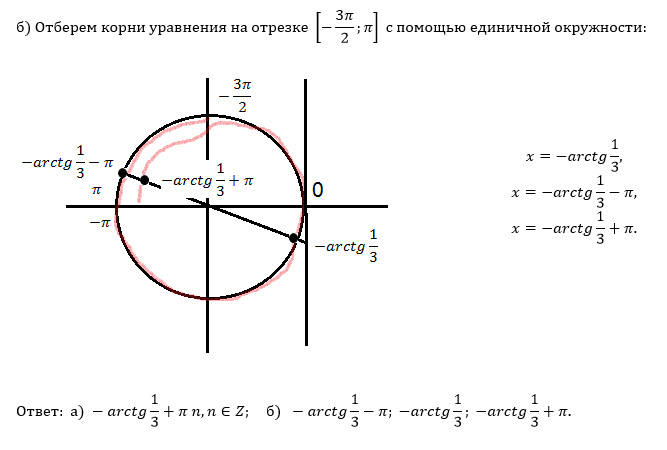
б) Найдите все корни уравнения, принадлежащие отрезку [-3Pi/2 ; Pi].

sova

2019-02-25 13:42:27

ОДЗ:
{cosx≠0 ( иначе tgx не существует)
{tg^2x+1 ≠ 0 , так как tg^2x ≥ 0 при условии первого неравенства

Так как
1+tg^2 α=1/cos^2 α
и
по формулам приведения
sin(3π+2x)=-sin2x

sin2x=2*sinx*cosx

Уравнение принимает вид:
2*cos^2x=-6sinx*cosx
2*cos^2x+6sinx*cosx=0
2cosx*(cosx+3sinx)=0

cosx ≠ 0 ( cм. ОДЗ)

cosx+3sinx=0
3sinx=-cosx - однородное уравнение первой степени, делим на sinx≠ 0

ctgx=-3
x=arcctg(-3)+πk, k ∈ Z
x= - arctg(3)+πk, k ∈ Z

A) О т в е т. - arctg(3)+πk, k ∈ Z

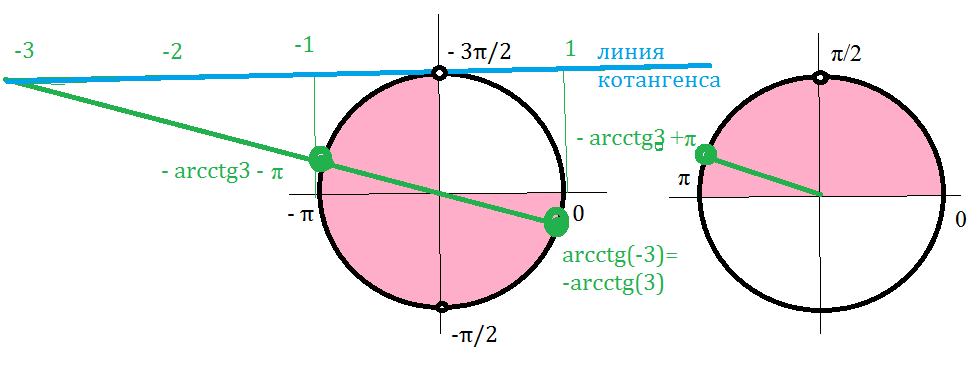
Б) Указанному отрезку принадлежат корни:
-arcctg3-π; -arcctg3; -arctg3+π

см. рис.
Так как указанный отрезок включает 5 раз по π/2
рисунок нарисовала отдельно
для [-3π/2;0] и для (0;π]