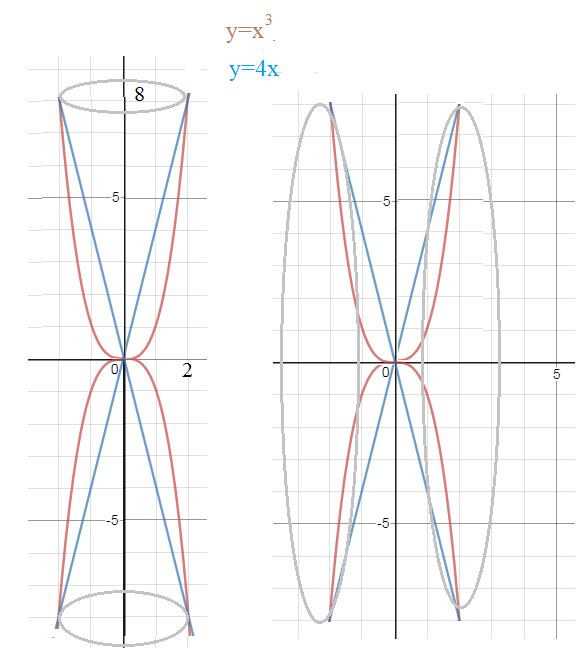
Задача 33789 Помогите пожалуйста....Найти...

vk457319503

2019-02-21 13:41:07

Помогите пожалуйста....Найти V(объем)образованный при вращении вокруг оси Ox и Oy плоских фигур ограниченных линиями

sova

2019-02-21 15:44:29

1. см. рис1
Считаем объем четвертой части и умножаем его на 4
V_(Ох)=4* π ∫^(2)_(0)((4x)^2-(x^3)^2)dx=
=4π * ∫^(2)_(0)(16x^2-x^6)dx=
=4π*((16x^3/3)-(x^7/7))|^(2)_(0)=
=4π*((128/3)-(128/7))=4π*128*((1/3)-(1/7))=512π*(4/21)=2048π/21
.
из уравнения y=4x выражаем переменную x=y/4
из уравнения y=x^3 выражаем переменную x=∛y
см. рис.2
V_(Оy)=4* π ∫^(8)_(0)((y/4)^2-(∛y)^2)dy=

=4π * ∫^(8)_(0)((y^2/16)-y^(2/3))dx=

=4π*((y^3/48)-(y^(5/3)/(5/3)))|^(8)_(0)=

=4π*((8^3/48)-(3/5)*∛8^5)=

=4π((64/6)-(3/5)*8∛16) - о т в е т.

2.
V_(Ох)= π ∫^(π)_(0)sin^2xdx=π ∫^(π)_(0)(1/2)*(1-cos2x)dx=

=(π/2)*(x- (1/2)sin2x)|^(π)_(0)=π^2/2

3.
(1/2)x^2-2x=0
(1/2)*x*(x-4)=0
x=0 или x=4

V_(Ох)= π ∫^(4)_(0)((1/2)x^2-2x)^2dx=π ∫^(4)_(0)((1/4)x^4-2x^3+4x^2)dx=

=((1/4)*(x^5/5) -2*(x^4/4)+4*(x^3/3))|^(4)_(0)=

=(1/20)*4^5-(1/2)*4^4+(4/3)*4^3=