Задача 33390 1.) исследовать с помощью элементарной...
Условие
1.область определения функции D(y)
2. Область изменения функции E(y)
3. Честность или нечетность функции
4.переодичность
5.нули функции
6.интервалы знака постоянства
2.) исследовать с помощью теории пределов
7.непрерывность функции
8.поведение функции на бесконечности (для этого вычислить пределы)
9.асимптоты граф. функции
3.) исследовать с помощью производной
10.экстремумы интервала
11.выпуклость, вогнутость функции в точках переживаю
4.) построение графика функции
12.найти точку пересечения с осью OY
13.дополнительные точки (4–6)
14.в системе координат XOY построить график функции
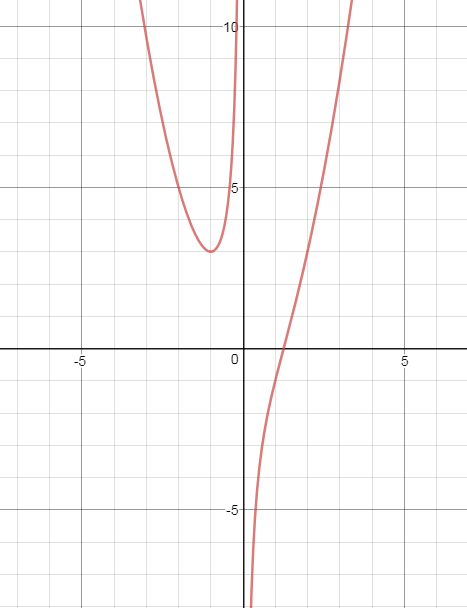
a.) y=x^3-2/3x
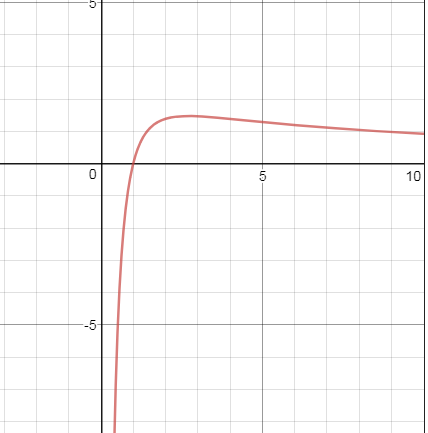
б.) y=4lnx/x
Решение
[b]y=(x^3-2)/3x[/b]
1.область определения функции D(y)=(- ∞ ;0) U(0; + ∞ )
2. Область изменения функции E(y) =(-∞ ; + ∞ )
см. рис.
3. Чётность или нечётность функции
f(-x)=((-x)^3-2)/(3*(-x))=(x^3+2)/(3x)
f(-x)≠ f(x)
f(-x) ≠ -f(x)
функция не является ни чЁтной ни нечЁтной
4.перИодичность - непериодическая
5.нули функции
y=0
x^3-2=0
x= ∛2
6.интервалы знака постоянства
___+__ (0) __-__( ∛2) ____+__
y > 0 при x< 0 и x > ∛2
y < 0 при 0 < x < ∛2
2.) исследовать с помощью теории пределов
7.непрерывность функции
непрерывна на области определения как частное непрерывных функций
8.поведение функции на бесконечности (для этого вычислить пределы)
lim_(x→+∞) y =+∞
lim_(x→ - ∞)y = +∞
9.асимптоты граф. функции
y=0 - вертикальная асимптота.
других асимптот нет.
3.) исследовать с помощью производной
y`=((3x^2)*3x-(3x)`*(x^3-2))/(3x)^2
y`=(9x^3-3x^3+6)/(9x^2)
y`=(6x^3+6)/9x^2
y`=0
x^3+1=0
x= - 1
_-__ (- 1) __+__(0) ___+_
Возрастает на (- 1 ; 0) и на (0; + ∞ )
Убывает на (- ∞ ; -1)
х= - 1 - точка минимума
y(-1)=((-1)^3-2)/3*(-1)=1
См. рис.1
б)
[b]y=(4lnx)/x[/b]
1.область определения функции D(y)=(0 ; + ∞ )
2. Область изменения функции E(y) =(- ∞;(4/e)]
см. рис.
3. Четность или нечетность функции
функция не является ни чЁтной ни нечЁтной
4.перИодичность - непериодическая
5.нули функции
y=0
4lnx=0
x=1
(1;0) - точка пересечения с осью Ох
6.интервалы знака постоянства
y > 0 при x >1
y < 0 при 0 < x < 1
2.) исследовать с помощью теории пределов
7.непрерывность функции
непрерывна на области определения, как частное непрерывных функций
8.поведение функции на бесконечности (для этого вычислить пределы)
lim_(x→+∞)(4lnx)/(x)=(∞/∞)
применяем правило Лопиталя
lim_(x→+∞) 4/(x)/1=0
lim_(x→ - ∞) не рассматриваем Согласно области определения
x > 0
9.асимптоты граф. функции
y=0 - горизонтальная асимптота на + ∞
x=0 - вертикальная асимптота ( справа)
3.) исследовать с помощью производной
y`=4*((lnx)`*x-(lnx)*x`)/(x^2)
y`=4*(1-lnx)/(x^2)
y`=
1-lnx=0
lnx=1
x=e
(0) ___+__ (e) __-__
Возрастает на (0;e)
Убывает на (e; + ∞ )
x=e - точка максимума
y(e)=4/e
См. рис.2