Задача 3326 В июле планируется взять кредит в банке...

slava191

10.08.2015

В июле планируется взять кредит в банке на сумму 10 млн рублей на 5 лет. Условия его возврата таковы:
- каждый январь долг возрастает на 10% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить часть долга;
- в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года.
Сколько млн рублей составила общая сумма выплат после погашения кредита?

1 год:

В январе сумма долга составит 10*1,1 = 11 млн. руб.

Пусть 1 платеж составил X млн. руб. Тогда после 1 платежа долг составит (11-X) млн. руб.

Так как в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года, то разница между долгом каждый год будет равна

10 - (11-X) = (X - 1) млн. руб.

Осталось выплатить долг еще за 4 года. Через 4 года долг в июле месяце будет равен

10 - 5*(X-1).

Так как кредит был погашен за 5 лет, то последний долг равен 0, т.е. получаем уравнение:

10 - 5*(X-1) = 0,

X-1 = 2,

X = 3.

То есть 1-ый платеж составил 3 млн. руб.

После этого долг в июле составил 11-3 = 8 млн. руб.

Во 2 год в январе долг составит уже 1,1*8 = 8,8 млн. руб. И так как разница между долгом каждый год в июле равна 3 - 1 = 2 млн. руб., то на июль 2-го года долг составит 8 - 2 = 6 млн. руб. Значит, 2 платеж был равен 8,8 - 6 = 2,8 млн. руб.

В 3 год в январе долг равен 1,1*6 = 6,6 млн. руб. На июль 3-го года долг будет равен 6 - 2 = 4 млн. руб., значит, 3 платеж равен 6,6 - 4 = 2,6 млн. руб.

В 4 год в январе долг равен 4*1,1 = 4,4 млн. руб. На июль 4 года долг составит 4 - 2 = 2 млн. руб. И 4-ый платеж был равен 4,4 - 2 = 2,4 млн. руб.

На январь 5-го года долг составит 2*1,1 = 2,2 млн. руб. И так как кредит был полностью погашен за 5 лет, то это будет последний платеж и он будет равен сумме долга, т.е. 2,2 млн. руб.

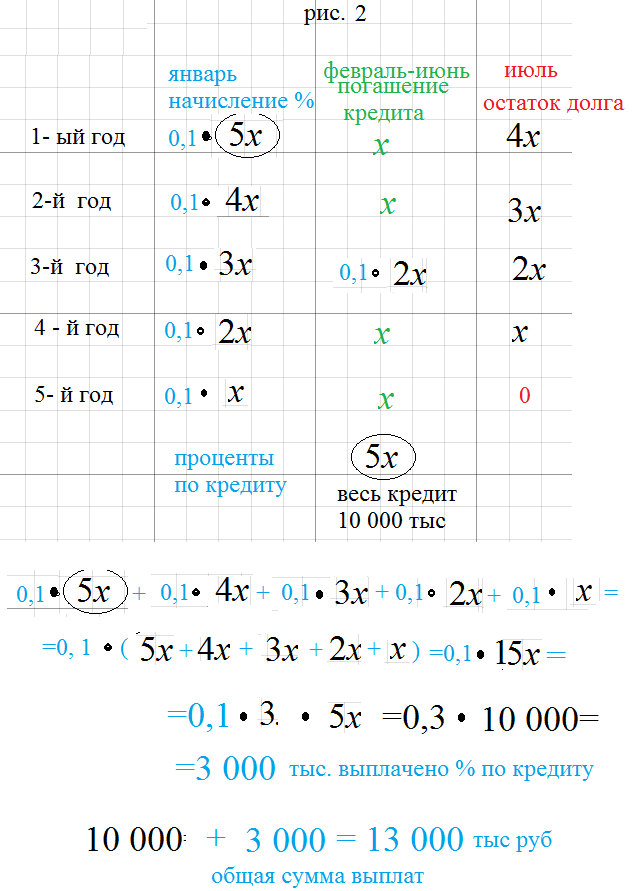
Итого общая сумма платежей за 5 лет составила: 3+2,8+2,6+2,4+2,2 = 13 млн. руб.

Ответ: 13

u109165758

12.01.2017

★

Пусть сумма кредита s.По условию, долг перед банком в июле каждого года должен быть на одну и ту же величину меньше,долга на июль предыдущего года.s;0,8s;0,6s;0,4s;0,2s;0.Пусть каждый январь долг возрастает на r%.Пусть k=1+0,01r,тогда последовательность размеров долга на каждый январь такая:ks;0,8ks;0,6ks;0,4ks0,2ks.Следовательно выплаты будут следующими:0,2s+s(k-1);0,8[(k-1)s+s];...0,2[(k-1)s+s].Всего следует выплатить:s+s(k-1)(1+0,8+0,6+0,4+0,2)=s+s(k-1)*3=s(1+3(k-1)).В нашем случае s=10 млн,k=1,1.Подставляя эти значения получаем 10*(1+3(1,1-1))=10*(1+0,3)=13.Ответ.13.

vk397114329

2019-02-18 00:04:53

Полная величина выплаты находим по формуле: В=s*(1+ r*(n+ 1)/200). где s-кредит,
r-годовая ставка, n-сколько лет. В нашем случае s=10 млн. руб, r=10%, n=5 лет.
в=10*(1+ 10*6/200)=10*1,3=13.
Ответ. 13.