Задача 32695 ...

89965026654

13 января 2019 г. в 17:04

Исследовать функцию y=(3(〖x+1)〗²)/(3x³–2x+3) и построить схематично её график. Задача № 6

sova

13 января 2019 г. в 18:48

★

Область определения (– ∞;+ ∞ )
y`=3(((x+1)<sup>2</sup>)`·(3x²–2x+3)–(x+1)²·(3x²–2x+3)`)/(3x²–2x+3)²

y`=3·(2·(x+1)·(x+1)`·(3x²–2x+3)–(x+1)²·(6x–2))/(3x²–2x+3)²

y`=0

(х+1)·(2(3x²–2x+3)–6x²–4x+2)=0

(х+1)·(–8х+8)=0

x=–1; x=1 – точки возможного экстремума

__–__ (–1) ___+__ (1) ___–__

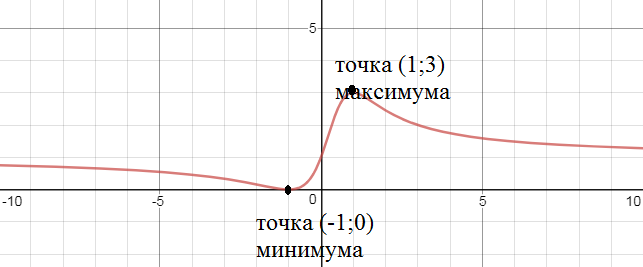
х=–1 – точка минимума
х=1– точка максимума

Есть горизонтальная асимптота
у=1
lim_x→∞y=1