Задача 32513 ...
Условие
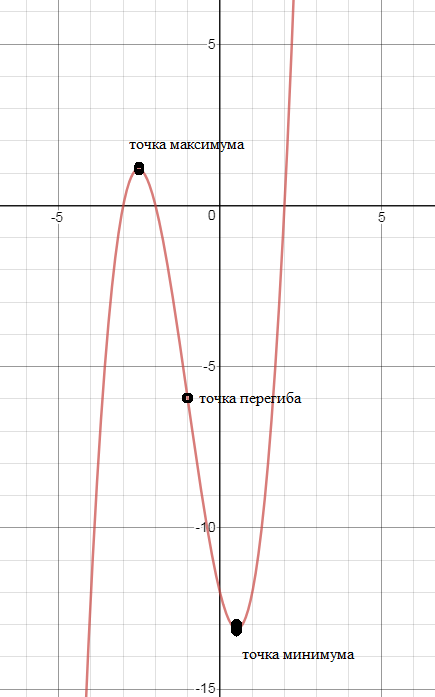
у = (x^2-4) ∙ (х +3)
математика
1157
Все решения
Находим производную
y`=(u*v)`=u`*v+u*v`=
=(x^2-4)`*(x+3)+(x^2-4)*(x+3)`=2x*(x+3)+(x^2-4)*1=
=3x^2+6x-4
y`=0
3x^2+6x-4=0
D=36+48=84
x_(1)=(-6-2sqrt(21))/6=-1-(sqrt(21)/3) или х_(2)=(-6+2sqrt(21))/6=-1+(sqrt(21)/3)
Расставляем знак производной:
__+___ (-1-(sqrt(21)/3)) ____-_____ (-1+(sqrt(21)/3)) ___+___
На (- ∞ ; (-1-(sqrt(21)/3)) и на ((-1+(sqrt(21)/3)) ;+ ∞ )
функция возрастает
на ((-1-(sqrt(21)/3) ; (-1+(sqrt(21)/3))
функция убывает
x=-1-(sqrt(21)/3) - точка максимума
x=-1+(sqrt(21)/3) - точка минимума
y``=6x+6
x=-1 - точка перегиба