Задача 32510 Исследовать функции и построить график,...
Условие
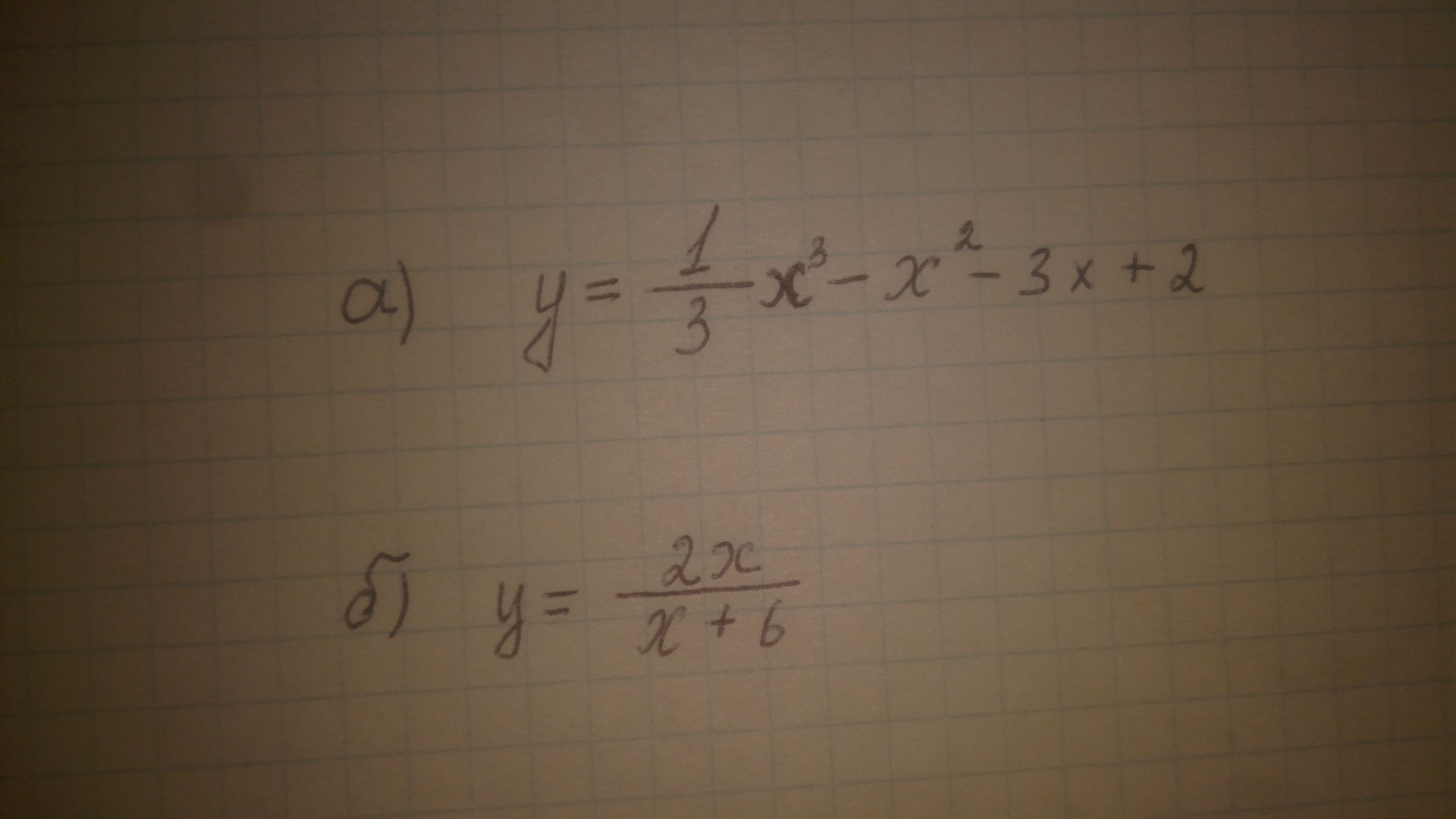
Решение
y`=x^2-2x-3
y`=0
x^2-2x-3=0
D=4+12=16
x_(1)=(2-4)/2=-1; x_(2)=(2+4)/2=3
__+__ (-1) __-___ (3) __+__
y`>0 на (- ∞ ;-1) и на (3;+ ∞ ), значит функция возрастает
y`< 0 на (-1 ;3), значит функция убывает
х=-1 - точка максимума, производная меняет знак с + на -
у(-1)=(1/3)*(-1)^3-(-1)^2-3*(-1)+2=(-1/3)+4=11/3
х=3 - точка минимума, производная меняет знак с - на +
y(3)=(1/3)*3^3-3^2-3*3+2=9-9-9+2= - 7
y``=2x-2
y``=0
2x-2=0
x=1- точка перегиба, вторая производная меняет знак с - на +
Функция выпукла вверх на ( (- ∞ ;1) и выпукла вниз на (1;+ ∞ )
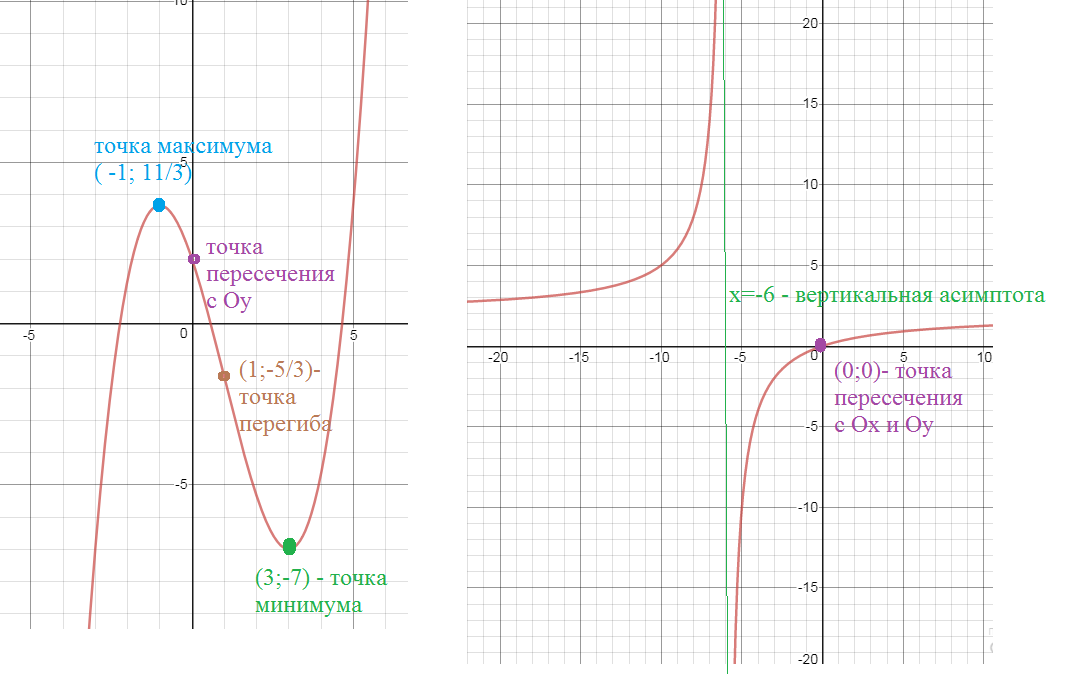
См. график рис. 1
б)
Область определения (- ∞ ;-6) U(-6;+ ∞ )
y`=(2*(x+6)-2x)/(x+6)^2
y`=12/(x+6)^2 > 0 при любом х из области определения, т.е
(- ∞ ;-6) U(-6;+ ∞ )
Функция возрастает на (- ∞ ;-6) и (-6;+ ∞ )
См. график рис. 2