Задача 32418 2 пожалуйста...

vk144321234

2018-12-25 10:12:54

2 пожалуйста

sova

2018-12-25 20:58:02

★

1.
Область определения х ≠ -3
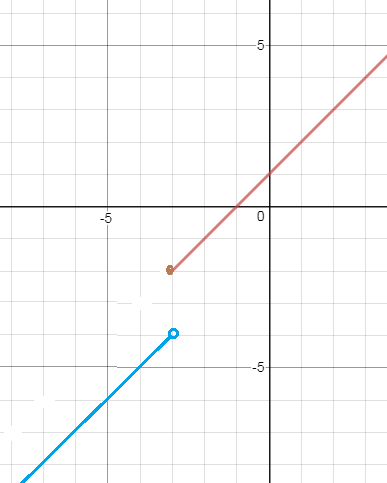
Значит исследуем точку x=-3

При x → -3 -0
|x+3|=-x-3
y=x+(x+3)/(-x-3)=x+1
Предел слева
f(-3-0)=lim_(x → -3 -0 )(x-1)=-4

При x → -3 +0
|x+3|=x+3
y=x+(x+3)/(x+3)=x+1
Предел справа
f(-3+0)=lim_(x → -3 +0 )(x+1)=-2

в точке х=-3 функция имеет разрыв первого рода.
Скачок функции конечный и равен
f(-3+0)-f(-3-0)2-(-4)=2

2.
Область определения х ≠± 4

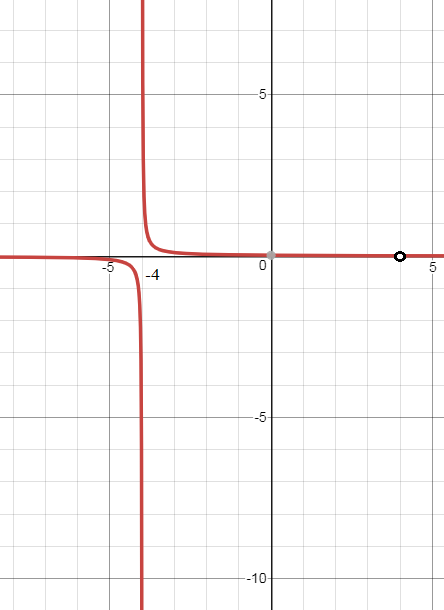
Значит исследуем точки x=-4 и х=4

х=-4

Предел слева
f(-4-0)=lim_(x → -4 -0 )f(x)=-∞
Предел справа
f(-4+0)=lim_(x → -4 +0 )f(x)=+ ∞

x=-4 - точка разрыва второго рода.


х=4

Предел слева
f(4-0)=lim_(x → 4 -0 )f(x)=(неопределенность0/0)
умножаем и числитель и знаменатель на (sqrt(21+x)+5)
lim_(x → 4 -0 )(x-4)/(x-4)(x+4)*sqrt((21+x)+5)=1/80

Предел справа
f(4+0)=lim_(x → 4 +0 )f(x)=(неопределенность0/0)
умножаем и числитель и знаменатель на (sqrt(21+x)+5)
lim_(x → 4 +0 )(x-4)/(x-4)(x+4)*sqrt((21+x)+5)=1/80

Предел слева равен пределу справа, но функция в точке х=4 не определена.

x=4 - точка устранимого разрыва