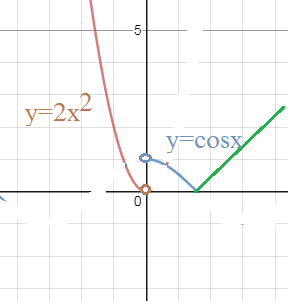Задача 32162 Найти точки разрыва функции. Изобразить...
Условие
Изобразить график функции в окрестности точки разрыва.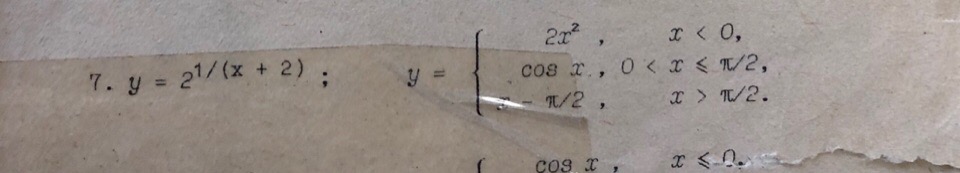
предмет не задан
1628
Решение
★
Область определения (- ∞ ;-2)U(-2;+ ∞ )
Исследуем точку х=-2
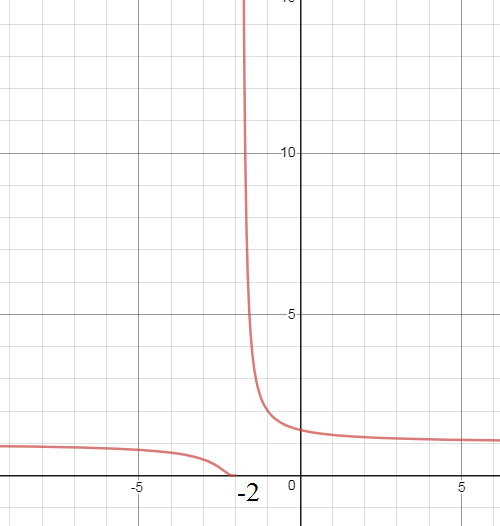
f(-2-0)= lim_(x→(-2-0)2^(1/(x+2))=2^(- ∞)=0
f(-2+0)= lim_(x→(-2+0)2^(1/(x+2))=2^(+ ∞)=+ ∞
х=-2 - точка разрыва второго рода
Рис. 1
2.
x=-0
f(-0)= lim_(x→(-0))2x^2=0
f(+0)= lim_(x→(+0))cosx=cos0=1
х=0 - точка разрыва первого рода
Есть конечный скачок
f(+0) -f(-0)=1
f((π/2)-0)= lim_(x→((π/2)-0)cosx=cos(π/2)=0
f((π/2)+0)= lim_(x→(+0)(x-(π/2))=0
f(0)=0
Предел слева равен пределу справа равен значению функции в точке.
x=π/2 - точка непрерывности